Exam 8: Drawing Inferences From Large Samples
Exam 1: Introduction to Statistics17 Questions
Exam 2: Organization and Description of Data53 Questions
Exam 3: Descriptive Study of Bivariate Data44 Questions
Exam 4: Probability54 Questions
Exam 5: Probability Distributions49 Questions
Exam 6: The Normal Distribution32 Questions
Exam 7: Variation in Repeated Samplessampling Distributions31 Questions
Exam 8: Drawing Inferences From Large Samples48 Questions
Exam 9: Small Sample Inferences for Normal Populations36 Questions
Exam 10: Comparing Two Treatments37 Questions
Exam 11: Regression Analysis I29 Questions
Exam 12: Regression Analysis II Multiple Linear Regression and Other Topics5 Questions
Exam 13: Analysis of Categorical Data19 Questions
Exam 14: Analysis of Variance Anova16 Questions
Exam 15: Nonparametric Inference15 Questions
Select questions type
An industrial researcher wants to perform a test with the intent of establishing that this company's compact fluorescent lamp has a mean life greater than 6300 hours. The sample size is 106 and he knows that =53 hours.
If he set the rejection region to be 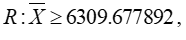 what is the level of significance of his test?
what is the level of significance of his test?
Free
(Short Answer)
4.7/5  (37)
(37)
Correct Answer:
.03
Consider the following statement,
The mean time of pregnancy is 287 days.
Suppose that the decision has been made to retain the null hypothesis
A) When is it a wrong decision?
B) What type of error is then made?
Free
(Essay)
4.8/5  (37)
(37)
Correct Answer:
Part A: or a value less than or greater than 287
Part B: Type II
Out of a sample of 645 students, 429 had binge watched a TV series last month.
Find a 95% confidence interval for the population proportion of purchases paid with credit or debit card.
Free
(Short Answer)
4.8/5  (38)
(38)
Correct Answer:
(.629, .702)
If the goal of the study is to establish that the mean amount of gasoline consumed by a S.U.V. in 100 miles of highway is over 8.5 gallons, the null and alternative hypotheses are:

(True/False)
4.7/5  (40)
(40)
A travel agency wants to estimate the proportion of cancellations per year they receive. How large a sample of records must be examined to be 86% sure that the estimate does not differ from the true proportion by more than 0.02? The travel agent knows that the proportion is about 29%
(Short Answer)
4.7/5  (46)
(46)
Given your claim about a population proportion, the sample size n, and the desired level of significance α.
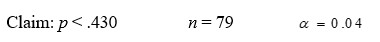 Formulate:
A) the hypotheses,
B) the test statistic Z,
C) the rejection region
Formulate:
A) the hypotheses,
B) the test statistic Z,
C) the rejection region
(Essay)
4.9/5  (39)
(39)
For the following data estimate.
A) The point estimate of μ.
B) The 100(1-α)% error margin.
n = 68 X̄=138 s=6 1-α= 0.86
(Essay)
4.8/5  (34)
(34)
Thirty-six measurements are made on the amount of meat in a pizza product. The summary statistics are
n = 36 = 17.4 grams s = 1.8 grams
Let µ =population mean amount of meat.
(a) Obtain a 98 % confidence interval for µ.
(b) Does your 98 % confidence interval cover µ. Explain.
(c) When a large number of these 98 % intervals are calculated, from data collected on different occasions, explain the reason you are 98% confident that any one of them covers µ. confi- dence that
(Essay)
4.8/5  (35)
(35)
Consider the problem of estimating , the mean time per day spent in the gym for freshmen students. Obtain the point estimate of and the estimated standard error.
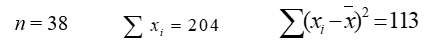 A)
A) 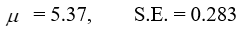 B)
B) 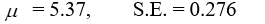 C)
C) 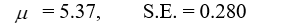 D)
D) 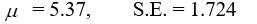
(Short Answer)
4.9/5  (41)
(41)
Employees of a movie theater ask their customers whether they like the movie exhibited or not. Out of 492 customers surveyed, 341 liked the movie. Compute a 88% confidence interval for the population proportion of satisfied customers.
(Short Answer)
4.8/5  (43)
(43)
In a study on the annual salary of recently graduated engineers, a random sample of 50 professional was taken. The sample mean and standard deviation were found to be $79,100 and $9200 respectively. Use these data to construct a 95% confidence interval for the mean annual salary of recently graduated engineers. Round your answer to the nearest integer.
(Essay)
4.9/5  (26)
(26)
A cell phone provider surveyed four hundred customers about sat- isfaction with their student service plan. The number that replied unsatisfactory, X, was recorded. The summary statistics are n =
400 x = 24. Let p =population proportion.
(a) Conduct a test of hypotheses with intent of showing that p /=
17. Take = .05.
(b) Explain your choice of sampling distribution.
(c) Sketch the null distribution of your statistic and the rejection region.
(d) Based on the conclusion to your test in Part a, what error could you have made?
(Essay)
5.0/5  (34)
(34)
A staff member of the office of institutional research in a large university wants to estimate the proportion of students that fail the Calculus I course. A faculty member mentioned to her that 35% of the students fail the course. How many academic reports should the staff member analyze to be 90% confident that the error estimation is within 0.03?
(Short Answer)
4.8/5  (35)
(35)
Given your claim about a population proportion, the sample size n, and the desired level of significance α.
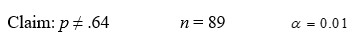 Formulate:
A) the hypotheses,
B) the test statistic Z,
C) the rejection region
Formulate:
A) the hypotheses,
B) the test statistic Z,
C) the rejection region
(Essay)
4.8/5  (41)
(41)
Thirty-six measurements are made on the amount of meat in a pizza product. The summary statistics are
n = 36 = 17.4 grams s = 1.8 grams
Let µ =population mean amount of meat.
(a) Conduct a test of hypotheses with the intent of showing that
µ /= 17. Take α = .05.
(b) Explain your choice of sampling distribution.
(c) Sketch the null distribution of your statistic and the rejection region.
(d) Based on the conclusion to your test in Part a, what error could you have made?
(Essay)
4.8/5  (41)
(41)
Consider the following statement,
The mean amount of money spent in leisure activities for a 4-number family in the east coast is less than $200 per month.
Suppose that the decision has been to reject the null hypothesis.
A)When is it a wrong decision?
B) What type of error is then made?
The mean amount of money spent in leisure activities for a 4-number family in the east coast is less than $200 per month.
(Essay)
4.9/5  (37)
(37)
Given your claim about a population proportion, the sample size n, and the desired level of significance α.
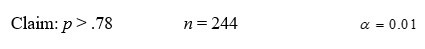 Formulate:
A) the hypotheses,
B) the test statistic Z,
C) the rejection region.
Formulate:
A) the hypotheses,
B) the test statistic Z,
C) the rejection region.
(Essay)
4.8/5  (33)
(33)
Determine the sample size n that is required for estimating the population mean. The population standard deviation and the desired error margin are specified.
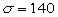 90% error margin 4
90% error margin 4
(Multiple Choice)
4.9/5  (33)
(33)
Showing 1 - 20 of 48
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)