Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 12: Regression Analysis II Multiple Linear Regression and Other Topics

arrow
Exam 1: Introduction to Statistics17 Questionsadd course
Exam 2: Organization and Description of Data53 Questionsadd course
Exam 3: Descriptive Study of Bivariate Data44 Questionsadd course
Exam 4: Probability54 Questionsadd course
Exam 5: Probability Distributions49 Questionsadd course
Exam 6: The Normal Distribution32 Questionsadd course
Exam 7: Variation in Repeated Samplessampling Distributions31 Questionsadd course
Exam 8: Drawing Inferences From Large Samples48 Questionsadd course
Exam 9: Small Sample Inferences for Normal Populations36 Questionsadd course
Exam 10: Comparing Two Treatments37 Questionsadd course
Exam 11: Regression Analysis I29 Questionsadd course
Exam 12: Regression Analysis II Multiple Linear Regression and Other Topics5 Questionsadd course
Exam 13: Analysis of Categorical Data19 Questionsadd course
Exam 14: Analysis of Variance Anova16 Questionsadd course
Exam 15: Nonparametric Inference15 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

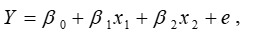Suppose the price, y, per ton of copper can be modeled by Suppose the price, y, per ton of copper can be modeled by where the two predictor variables x<sub>1</sub> and x<sub>2</sub> are the prices per ton of zinc and lead, respectively. The least squares estimates, based on monthly observations in a five-year period, are: Assuming that the residual sum of squares (SSE) is 1424.48 and the SS due to regression is 5150.68. A) Estimate the error standard deviation. B) State the degrees of freedom used in part A. C) Find R<sup>2</sup>. where the two predictor variables x1 and x2 are the prices per ton of zinc and lead, respectively. The least squares estimates, based on monthly observations in a five-year period, are: 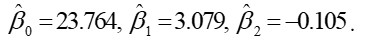Suppose the price, y, per ton of copper can be modeled by where the two predictor variables x<sub>1</sub> and x<sub>2</sub> are the prices per ton of zinc and lead, respectively. The least squares estimates, based on monthly observations in a five-year period, are: Assuming that the residual sum of squares (SSE) is 1424.48 and the SS due to regression is 5150.68. A) Estimate the error standard deviation. B) State the degrees of freedom used in part A. C) Find R<sup>2</sup>. Assuming that the residual sum of squares (SSE) is 1424.48 and the SS due to regression is 5150.68. A) Estimate the error standard deviation. B) State the degrees of freedom used in part A. C) Find R2.

Free
(Essay)
4.7/5
(38)
Question 1
Correct Answer:
Verified

Part A: 24.301
Part B: 57
Part C: 0.783

Consider the data set Consider the data set A) Obtain the best fitting straight line with B) What proportion of the y'variability is explained by the fitted line? Round your answers to three decimal places. A) Obtain the best fitting straight line with Consider the data set A) Obtain the best fitting straight line with 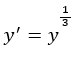B) What proportion of the y'variability is explained by the fitted line? Round your answers to three decimal places. B) What proportion of the y'variability is explained by the fitted line? Round your answers to three decimal places.

Free
(Essay)
4.8/5
(34)
Question 2
Correct Answer:
Verified

Part A: Part A: 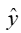= .180 - 1.940x Part B: .993= .180 - 1.940x
Part B: .993

Find a linearizing transformation of y=1/(a + b x)

Free
(Short Answer)
4.8/5
(43)
Question 3
Correct Answer:
Verified

y' = 1/y, x' = x

Suppose the price, y, per ton of copper can be modeled by 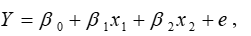Suppose the price, y, per ton of copper can be modeled by where the two predictor variables x<sub>1</sub> and x<sub>2</sub> are the prices per ton of zinc and lead, respectively. The least squares estimates are: Predict the response for x<sub>1</sub>= 2389 and x<sub>2</sub> = 2366. where the two predictor variables x1 and x2 are the prices per ton of zinc and lead, respectively. The least squares estimates are: 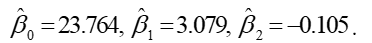Suppose the price, y, per ton of copper can be modeled by where the two predictor variables x<sub>1</sub> and x<sub>2</sub> are the prices per ton of zinc and lead, respectively. The least squares estimates are: Predict the response for x<sub>1</sub>= 2389 and x<sub>2</sub> = 2366. Predict the response for x1= 2389 and x2 = 2366.

(Short Answer)
4.8/5
(42)
Question 4

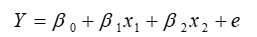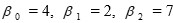Consider the multiple linear regression model Consider the multiple linear regression model where , and the normal random variable e has standard deviation 6. What is the mean of the response Y when x<sub>1</sub> = 1 and x<sub>2</sub> = 4? where Consider the multiple linear regression model where , and the normal random variable e has standard deviation 6. What is the mean of the response Y when x<sub>1</sub> = 1 and x<sub>2</sub> = 4? , and the normal random variable e has standard deviation 6. What is the mean of the response Y when x1 = 1 and x2 = 4?

(Multiple Choice)
4.8/5
(37)
Question 5
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)