Exam 5: Utility and Game Theory
Exam 1: Introduction61 Questions
Exam 2: Introduction to Probability66 Questions
Exam 3: Probability Distributions66 Questions
Exam 4: Decision Analysis64 Questions
Exam 5: Utility and Game Theory67 Questions
Exam 6: Times Series Analysis and Forecasting63 Questions
Exam 7: Introduction to Linear Programming60 Questions
Exam 8: Linear Programming: Sensitivity Analysis and Interpretation of Solution64 Questions
Exam 9: Linear Programming Applications in Marketing, Finance, and Operations Management60 Questions
Exam 10: Distribution and Network Models67 Questions
Exam 11: Integer Linear Programming61 Questions
Exam 12: Advanced Optimization Applications56 Questions
Exam 13: Project Scheduling: Pertcpm66 Questions
Exam 14: Inventory Models66 Questions
Exam 15: Waiting Line Models62 Questions
Exam 16: Simulation62 Questions
Exam 17: Markov Processes55 Questions
Select questions type
For a two-person zero-sum game,which one of the following is false?
Free
(Multiple Choice)
4.7/5  (39)
(39)
Correct Answer:
C
Utility reflects the decision maker's attitude toward
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
B
A game has a pure strategy solution when both players' single-best strategies are the same.
Free
(True/False)
4.9/5  (41)
(41)
Correct Answer:
False
When the payoffs become extreme,most decision makers are satisfied with the decision that provides the best expected monetary value.
(True/False)
4.8/5  (40)
(40)
Determine decision strategies based on expected value and on expected utility for this decision tree.Use the utility function Payoff Indifference Probability 500 1.00 350 .89 300 .84 180 .60 100 .43 40 .20 20 .13 0 0 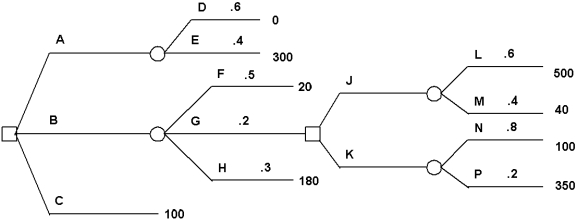
(Essay)
4.9/5  (45)
(45)
Consider the following two-person zero-sum game.Assume the two players have the same three strategy options.The payoff table below shows the gains for Player A. Player B Plaver Strategy Strategy Strategy Strategy 3 2 -4 Strategy -1 0 2 Strategy 4 5 -3 Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically? What is the value of the game?
(Essay)
4.9/5  (31)
(31)
The expected utility is the utility of the expected monetary value.
(True/False)
4.7/5  (38)
(38)
If a game larger than 2 X 2 requires a mixed strategy,we attempt to reduce the size of the game by
(Multiple Choice)
4.8/5  (31)
(31)
When the utility function for a risk-neutral decision maker is graphed (with monetary value on the horizontal axis and utility on the vertical axis),the function appears as
(Multiple Choice)
4.9/5  (31)
(31)
A game has a saddle point when pure strategies are optimal for both players.
(True/False)
4.8/5  (36)
(36)
Explain the relationship between expected utility,probability,payoff,and utility.
(Essay)
5.0/5  (33)
(33)
Consider a two-person,zero-sum game where the payoffs listed below are the winnings for Company X.Identify the pure strategy solution.What is the value of the game? Company Y Strategies Company X Strategies 3 5 9 8 4 3 7 6 7
(Essay)
4.8/5  (38)
(38)
Suppose that there are only two vehicle dealerships (A and B)in a small city.Each dealership is considering three strategies that are designed to take sales of new vehicles from the other dealership over a period of four months.The strategies,assumed to be the same for both dealerships,are:
Strategy 1: Offer a cash rebate on a new vehicle.
Strategy 2: Offer free optional equipment on a new vehicle.
Strategy 3: Offer a 0% loan on a new vehicle.
The payoff table (in number of new vehicle sales gained per week by Dealership A (or lost by Dealership B)is shown below. Dealership B Cash Rebate Free Options 0\% Loan Dealership A Cash Rebate 2 2 1 Free Options -3 3 -1 0\% Loan 3 -2 0 Identify the pure strategy for this two-person zero-sum game.What is the value of the game?
(Essay)
4.9/5  (36)
(36)
If the maximin and minimax values are not equal in a two-person zero-sum game,
(Multiple Choice)
4.9/5  (31)
(31)
When the decision maker prefers a guaranteed payoff value that is smaller than the expected value of the lottery,the decision maker is
(Multiple Choice)
4.8/5  (40)
(40)
Metropolitan Cablevision has the choice of using one of three DVR systems.Profits are believed to be a function of customer acceptance.The payoff to Metropolitan for the three systems is: System High \ 150,000 \ 200,000 \ 200,000 Medium \ 80,000 \ 20,000 \ 80,000 Low \ 20,000 -\ 50,000 -\ 100,000 The probabilities of customer acceptance for each system are: System High .4 .3 .3 Medium .3 .4 .5 Low .3 .3 .2 The first vice president believes that the indifference probabilities for Metropolitan should be: Amount Probability \ 150,000 .90 \ 80,000 .70 \ 20,000 .50 -\ 50,000 .25 The second vice president believes Metropolitan should assign the following utility values: Amount Utility \ 200,000 125 \ 150,000 95 \ 80,000 55 \ 20,000 30 -\ 50,000 10 -\ 100,000 0
a. Which vice president is a risk taker? Which one is risk averse?
b. Which system will each vice president recommend?
c. What system would a risk neutral vice president recommend?
(Essay)
5.0/5  (34)
(34)
A 3 x 3 two-person zero-sum game that has no optimal pure strategy and no dominated strategies
(Multiple Choice)
4.8/5  (32)
(32)
For a two-person,zero-sum,mixed-strategy game,each player selects its strategy according to
(Multiple Choice)
4.9/5  (37)
(37)
The utility function for a risk avoider typically shows a diminishing marginal return for money.
(True/False)
4.8/5  (44)
(44)
Showing 1 - 20 of 67
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)