Question 1

Explain how integer and 0-1 variables can be used in an objective function to minimize the sum of fixed and variable costs for production on two machines.

Accepted Answer

Integer and 0-1 variables can be used in an objective function to minimize the sum of fixed and variable costs for production on two machines by representing the decision variables for the production process.

The integer variables can represent the number of units produced on each machine, as production quantities are typically whole numbers. These integer variables can be used to determine the production levels on each machine in order to minimize the total cost.

The 0-1 variables can be used to represent whether a particular machine is used or not. For example, if a 0-1 variable is set to 1, it indicates that the machine is being used for production, while a value of 0 indicates that the machine is not being used. By including these 0-1 variables in the objective function, the model can determine the most cost-effective allocation of production across the two machines.

By including both integer and 0-1 variables in the objective function, the model can optimize the production process to minimize the sum of fixed and variable costs while meeting production requirements. This approach allows for a more accurate representation of the production process and can lead to significant cost savings for the company.

Question 2

To perform sensitivity analysis involving an integer linear program,it is recommended to

Accepted Answer

A) use the dual prices very cautiously. 
B) make multiple computer runs. 
C) use the same approach as you would for a linear program. 
D) use LP relaxation. 
A) use the dual prices very cautiously. 
B) make multiple computer runs. 
C) use the same approach as you would for a linear program. 
D) use LP relaxation. B

Question 3

Market Pulse Research has conducted a study for Lucas Furniture on some designs for a new commercial office desk.Three attributes were found to be most influential in determining which desk is most desirable: number of file drawers,the presence or absence of pullout writing boards,and simulated wood or solid color finish.Listed below are the part-worths for each level of each attribute provided by a sample of 7 potential Lucas customers. 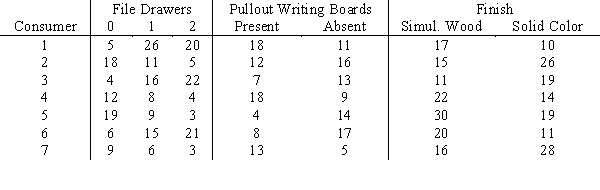  Suppose the overall utility (sum of part-worths)of the current favorite commercial office desk is 50 for each customer.What is the product design that will maximize the share of choices for the seven sample participants? Formulate and solve,using Lindo or Excel,this 0 - 1 integer programming problem.

Accepted Answer

Define the decision variables:
There are

7 l _ { i j }

decision variables, one for each level of attribute.

l _ { i j } = 1

if Lucas chooses level

i

for attribute

j ; 0

otherwise.
There are

7 Y _ { k }

decision variables, one for each consumer in the sample.

Y _ { k } = 1

if consumer

k

chooses the Lucas brand, 0 otherwise.

Define the objective function:
Maximize the number of consumers preferring the Lucas brand desk.

\operatorname { Max } \quad Y _ { 1 } + Y _ { 2 } + Y _ { 3 } + Y _ { 4 } + Y _ { 5 } + Y _ { 6 } + Y _ { 7 }

Define the constraints:
There is one constraint for each consumer in the sample.

\begin{array} { c } 5 l _ { 11 } + 26 l _ { 21 } + 20 l _ { 31 } + 18 l _ { 12 } + 11 l _ { 22 } + 17 l _ { 13 } + 10 l _ { 23 } - 50 Y _ { 1 } \geq 1 \\18 l _ { 11 } + 11 l _ { 21 } + 5 l _ { 31 } + 12 l _ { 12 } + 16 l _ { 22 } + 15 l _ { 13 } + 26 l _ { 23 } - 50 Y _ { 2 } \geq 1 \\4 l _ { 11 } + 16 l _ { 21 } + 22 l _ { 31 } + 7 l _ { 12 } + 13 l _ { 22 } + 11 l _ { 13 } + 19 l _ { 23 } - 50 Y _ { 3 } \geq 1 \\12 l _ { 11 } + 8 l _ { 21 } + 4 l _ { 31 } + 18 l _ { 12 } + 9 l _ { 22 } + 22 l _ { 13 } + 14 l _ { 23 } - 50 Y _ { 4 } \geq 1 \\19 l _ { 11 } + 9 l _ { 21 } + 3 l _ { 31 } + 4 l _ { 12 } + 14 l _ { 22 } + 30 l _ { 13 } + 19 l _ { 23 } - 50 Y _ { 5 } \geq 1 \\6 l _ { 11 } + 15 l _ { 21 } + 21 l _ { 31 } + 8 l _ { 12 } + 17 l _ { 22 } + 20 l _ { 13 } + 11 l _ { 23 } - 50 Y _ { 6 } \geq 1 \\9 l _ { 11 } + 6 l _ { 21 } + 3 l _ { 31 } + 13 l _ { 12 } + 5 l _ { 22 } + 16 l _ { 13 } + 28 l _ { 23 } - 50 Y _ { 7 } \geq 1\end{array}

There is one constraint for each attribute.

\begin{array} { l } l _ { 11 } + l _ { 21 } + l _ { 31 } = 1 \\l _ { 12 } + l _ { 22 } = 1 \\l _ { 13 } + l _ { 23 } = 1\end{array}

Optimal Solution:
Lucas should choose these product features:

1 file drawer

\left( I _ { 21 } = 1 \right)

No pullout writing boards

\left( I _ { 22 } = 1 \right)

Simulated wood finish

\left( I _ { 13 } = 1 \right)

Three sample participants would choose the Lucas design:
Participant

1 \left( Y _ { 1 } = 1 \right)

Participant

5 \left( Y _ { 5 } = 1 \right)

Participant

6 \left( Y _ { 6 } = 1 \right)

Question 4

If a problem has only less-than-or-equal-to constraints with positive coefficients for the variables,rounding down will always provide a feasible integer solution.

Accepted Answer

A) True 
 B)False

Question 5

Given the following all-integer linear programming problem:

$$\begin{array} { l } 
\operatorname { Max } \quad 3 x _ { 1 } + 10 x _ { 2 } \\
\text { s.t. } 2 x _ { 1 } + x _ { 2 } \leq 5 \
x _ { 1 } + 6 x _ { 2 } \leq 9 \
\begin{aligned}
x _ { 1 } - x _ { 2 } & \geq 2 \
x _ { 1 } , x _ { 2 } & \geq 0 \text { and integer }
\end{aligned} \
\end{array}$$ 
a. Solve the problem graphically as a linear program.
b. Show that there is only one integer point and it is optimal.
c. Suppose the third constraint was changed to x1 - x2 > 2.1. What is the new optimal solution to the LP? ILP?

Accepted Answer

a.x₁ = 7/3,x₂ = 1/3,obj.func.= 3

Question 6

In a model involving fixed costs,the 0 - 1 variable guarantees that the capacity is not available unless the cost has been incurred.

Accepted Answer

A) True 
 B)False

Question 7

In an all-integer linear program,

Accepted Answer

A) all objective function coefficients must be integer. 
B) all right-hand side values must be integer. 
C) all variables must be integer. 
D) all objective function coefficients and right-hand side values must be integer. 
A) all objective function coefficients must be integer. 
B) all right-hand side values must be integer. 
C) all variables must be integer. 
D) all objective function coefficients and right-hand side values must be integer.

Question 8

Assuming W1,W2 and W3 are 0 - 1 integer variables,the constraint W1 + W2 + W3 < 1 is often called a

Accepted Answer

A) multiple-choice constraint 
B) mutually exclusive constraint 
C) k out of n alternatives constraint 
D) corequisite constraint 
A) multiple-choice constraint 
B) mutually exclusive constraint 
C) k out of n alternatives constraint 
D) corequisite constraint

Question 9

Let x1 ,x2 ,and x3 be 0 - 1 variables whose values indicate whether the projects are not done (0)or are done (1).Which answer below indicates that at least two of the projects must be done?

Accepted Answer

A) x1 + x2 + x3 F1F1F1S1F1F1F10 2 
B) x1 + x2 + x3 F1F1F1S1F1F1F10 2 
C) x1 + x2 + x3 = 2 
D) x1 F1F1F1S1F1F1F10 x2 = 0 
A) x1 + x2 + x3 F1F1F1S1F1F1F10 2 
B) x1 + x2 + x3 F1F1F1S1F1F1F10 2 
C) x1 + x2 + x3 = 2 
D) x1 F1F1F1S1F1F1F10 x2 = 0

Question 10

Dual prices cannot be used for integer programming sensitivity analysis because they are designed for linear programs.

Accepted Answer

A) True 
 B)False

Question 11

The graph of a problem that requires x1 and x2 to be integer has a feasible region

Accepted Answer

A) the same as its LP relaxation. 
B) of dots. 
C) of horizontal stripes. 
D) of vertical stripes. 
A) the same as its LP relaxation. 
B) of dots. 
C) of horizontal stripes. 
D) of vertical stripes.

Question 12

If Project 5 must be completed before Project 6,the constraint would be x5 F1F1F1S1F1F1F10 x6 F1F1F1S1F1F1F10 0.

Accepted Answer

A) True 
 B)False

Question 13

Which of the following applications modeled in the textbook does not involve only 0 - 1 integer variables?

Accepted Answer

A) supply chain design 
B) bank location 
C) capital budgeting 
D) product design and market share optimization 
A) supply chain design 
B) bank location 
C) capital budgeting 
D) product design and market share optimization

Question 14

In a model,x1 F1F1F1S1F1F1F10 0 and integer,x2 F1F1F1S1F1F1F10 0,and x3 = 0,1.Which solution would not be feasible?

Accepted Answer

A) x1 = 5, x2 = 3, x3 = 0 
B) x1 = 4, x2 = .389, x3 = 1 
C) x1 = 2, x2 = 3, x3 = .578 
D) x1 = 0, x2 = 8, x3 = 0 
A) x1 = 5, x2 = 3, x3 = 0 
B) x1 = 4, x2 = .389, x3 = 1 
C) x1 = 2, x2 = 3, x3 = .578 
D) x1 = 0, x2 = 8, x3 = 0

Question 15

Tom's Tailoring has five idle tailors and four custom garments to make.The estimated time (in hours)it would take each tailor to make each garment is listed below.(An 'X' in the table indicates an unacceptable tailor-garment assignment.) $\quad $$\quad $$\quad $$\quad $$\quad $$\quad $$\quad $$\quad $$\quad $$\quad $$\quad $$\quad $$\quad $$\quad $$\quad $$\quad $$\text { Tail or }$
$$\begin{array} { l c c c c c } 
\text { Garment } & 1 & 2 & 3 & 4 & 5 \
\hline \text { Wedding gown } & 19 & 23 & 20 & 21 & 18 \
\text { Clown costume } & 11 & 14 & \mathrm { X } & 12 & 10 \
\text { Admiral's uni form } & 12 & 8 & 11 & \mathrm { X } & 9 \
\text { Bullfighter's outfit } & \mathrm { X } & 20 & 20 & 18 & 21
\end{array}$$ Formulate and solve an integer program for determining the tailor-garment assignments that minimize the total estimated time spent making the four garments.No tailor is to be assigned more than one garment and each garment is to be worked on by only one tailor.

Accepted Answer

The answer of Tom's Tailoring has five idle tailors and...

Question 16

Simplon Manufacturing must decide on the processes to use to produce 1650 units.If machine 1 is used,its production will be between 300 and 1500 units.Machine 2 and/or machine 3 can be used only if machine 1's production is at least 1000 units.Machine 4 can be used with no restrictions. $$\begin{array} { c c c c c } 
\text { Machine } & \begin{array} { c } 
\text { Fixed } \
\text { cost }
\end{array} & \begin{array} { c } 
\text { Variable } \
\text { cost }
\end{array} & \begin{array} { c } 
\text { Minimum } \
\text { Production }
\end{array} & \begin{array} { c } 
\text { Maximum } \
\text { Production }
\end{array} \
\hline 1 & 500 & 2.00 & 300 & 1500 \
2 & 800 & 0.50 & 500 & 1200 \
3 & 200 & 3.00 & 100 & 800 \
4 & 50 & 5.00 & \text { any } & \text { any }
\end{array}$$ (HINT: Use an additional 0 - 1 variable to indicate when machines 2 and 3 can be used.)

Accepted Answer

The answer of Simplon Manufacturing must decide on the processes...

Question 17

The constraint x1 + x2 + x3 + x4 F1F1F1S1F1F1F10 2 means that two out of the first four projects must be selected.

Accepted Answer

A) True 
 B)False

Question 18

Rounding the solution of an LP Relaxation to the nearest integer values provides

Accepted Answer

A) a feasible but not necessarily optimal integer solution. 
B) an integer solution that is optimal. 
C) an integer solution that might be neither feasible nor optimal. 
D) an infeasible solution. 
A) a feasible but not necessarily optimal integer solution. 
B) an integer solution that is optimal. 
C) an integer solution that might be neither feasible nor optimal. 
D) an infeasible solution.

Question 19

Sensitivity analysis for integer linear programming

Accepted Answer

A) can be provided only by computer. 
B) has precisely the same interpretation as that from linear programming. 
C) does not have the same interpretation and should be disregarded. 
D) is most useful for 0 - 1 models. 
A) can be provided only by computer. 
B) has precisely the same interpretation as that from linear programming. 
C) does not have the same interpretation and should be disregarded. 
D) is most useful for 0 - 1 models.

Question 20

Your express package courier company is drawing up new zones for the location of drop boxes for customers.The city has been divided into the seven zones shown below.You have targeted six possible locations for drop boxes.The list of which drop boxes could be reached easily from each zone is listed below. $\begin{array}{c}
\begin{array}{lll}
\text {Zone}\
\hline\text {Downtown Financial}\
\text {Downtown Legal}\
\text {Retail South}\
\text {Retail East}\
\text {Manufacturing North}\
\text {Manufacturing East}\
\text {Corporate West}\
\end{array}
\begin{array}{c}
\text {Can Be Served By Locations:}\
\hline1,2,5,6 \
2,4,5 \
1,2,4,6 \
3,4,5 \
1,2,5 \
3,4 \
1,2,6
\end{array}
\end{array}$
 Let xi = 1 if drop box location i is used,0 otherwise.Develop a model to provide the smallest number of locations yet make sure that each zone is covered by at least two boxes.

Accepted Answer

Explain how integer and 0-1 variables can be used in an objective function to minimize the sum of fixed and variable costs for production on two machines.

To perform sensitivity analysis involving an integer linear program,it is recommended to

If a problem has only less-than-or-equal-to constraints with positive coefficients for the variables,rounding down will always provide a feasible integer solution.

In a model involving fixed costs,the 0 - 1 variable guarantees that the capacity is not available unless the cost has been incurred.

In an all-integer linear program,

Assuming W₁,W₂ and W₃ are 0 - 1 integer variables,the constraint W₁ + W₂ + W₃ < 1 is often called a

Let x₁ ,x₂ ,and x₃ be 0 - 1 variables whose values indicate whether the projects are not done (0)or are done (1).Which answer below indicates that at least two of the projects must be done?

Dual prices cannot be used for integer programming sensitivity analysis because they are designed for linear programs.

The graph of a problem that requires x₁ and x₂ to be integer has a feasible region

If Project 5 must be completed before Project 6,the constraint would be x₅  x₆  0.

Which of the following applications modeled in the textbook does not involve only 0 - 1 integer variables?

In a model,x₁  0 and integer,x₂  0,and x₃ = 0,1.Which solution would not be feasible?

The constraint x₁ + x₂ + x₃ + x₄  2 means that two out of the first four projects must be selected.

Rounding the solution of an LP Relaxation to the nearest integer values provides

Sensitivity analysis for integer linear programming

Introduction

Introduction to Probability

Probability Distributions

Decision Analysis

Utility and Game Theory

Times Series Analysis and Forecasting

Introduction to Linear Programming

Linear Programming: Sensitivity Analysis and Interpretation of Solution

Linear Programming Applications in Marketing, Finance, and Operations Management

Distribution and Network Models

Advanced Optimization Applications

Project Scheduling: Pertcpm

Inventory Models

Waiting Line Models

Simulation

Markov Processes

Filters

Exam 11: Integer Linear Programming

Explain how integer and 0-1 variables can be used in an objective function to minimize the sum of fixed and variable costs for production on two machines.

To perform sensitivity analysis involving an integer linear program,it is recommended to

If a problem has only less-than-or-equal-to constraints with positive coefficients for the variables,rounding down will always provide a feasible integer solution.

In a model involving fixed costs,the 0 - 1 variable guarantees that the capacity is not available unless the cost has been incurred.

In an all-integer linear program,

Assuming W1,W2 and W3 are 0 - 1 integer variables,the constraint W1 + W2 + W3 < 1 is often called a

Let x1 ,x2 ,and x3 be 0 - 1 variables whose values indicate whether the projects are not done (0)or are done (1).Which answer below indicates that at least two of the projects must be done?

Dual prices cannot be used for integer programming sensitivity analysis because they are designed for linear programs.

The graph of a problem that requires x1 and x2 to be integer has a feasible region

If Project 5 must be completed before Project 6,the constraint would be x5  x6  0.

Which of the following applications modeled in the textbook does not involve only 0 - 1 integer variables?

In a model,x1  0 and integer,x2  0,and x3 = 0,1.Which solution would not be feasible?

The constraint x1 + x2 + x3 + x4  2 means that two out of the first four projects must be selected.

Rounding the solution of an LP Relaxation to the nearest integer values provides

Sensitivity analysis for integer linear programming

Introduction

Introduction to Probability

Probability Distributions

Decision Analysis

Utility and Game Theory

Times Series Analysis and Forecasting

Introduction to Linear Programming

Linear Programming: Sensitivity Analysis and Interpretation of Solution

Linear Programming Applications in Marketing, Finance, and Operations Management

Distribution and Network Models

Advanced Optimization Applications

Project Scheduling: Pertcpm

Inventory Models

Waiting Line Models

Simulation

Markov Processes

Filters

Assuming W₁,W₂ and W₃ are 0 - 1 integer variables,the constraint W₁ + W₂ + W₃ < 1 is often called a

Let x₁ ,x₂ ,and x₃ be 0 - 1 variables whose values indicate whether the projects are not done (0)or are done (1).Which answer below indicates that at least two of the projects must be done?

The graph of a problem that requires x₁ and x₂ to be integer has a feasible region

If Project 5 must be completed before Project 6,the constraint would be x₅  x₆  0.

In a model,x₁  0 and integer,x₂  0,and x₃ = 0,1.Which solution would not be feasible?

The constraint x₁ + x₂ + x₃ + x₄  2 means that two out of the first four projects must be selected.