Exam 13: Project Scheduling: Pertcpm
From this PERT/CPM network,determine the list of activities and their predecessors. 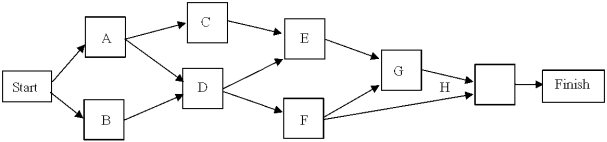
Once the earliest and latest times are calculated,how is the critical path determined?
The critical path in project management refers to the sequence of stages determining the minimum time needed to complete a project. Once the earliest start (ES) and latest finish (LF) times for each task are calculated, the critical path can be determined by following these steps:
1. **Identify Dependencies**: List all the tasks required to complete the project and identify the dependencies between tasks. This means understanding which tasks must be completed before others can start.
2. **Calculate Duration**: For each task, calculate the duration it will take to complete. This is typically given or estimated during the planning phase.
3. **Determine Earliest Start (ES) and Earliest Finish (EF) Times**: Using the forward pass method, calculate the ES and EF for each task. The ES for the first task is typically zero, and the EF is its duration. For subsequent tasks, the ES is the maximum EF of all its predecessor tasks, and the EF is the ES plus the task duration.
4. **Determine Latest Finish (LF) and Latest Start (LS) Times**: Using the backward pass method, calculate the LF and LS for each task. The LF for the final task is its EF. For preceding tasks, the LF is the minimum LS of all its successor tasks, and the LS is the LF minus the task duration.
5. **Calculate Slack or Float**: For each task, calculate the slack or float by subtracting the ES from the LS or the EF from the LF. Slack is the amount of time that a task can be delayed without affecting the project completion date.
6. **Identify the Critical Path**: The critical path is the sequence of tasks that have zero slack. These tasks cannot be delayed without affecting the project's completion date. To identify the critical path, look for the longest path through the network diagram or the path with tasks where the ES equals the LS and the EF equals the LF.
7. **Verify the Critical Path**: Double-check the calculations and the sequence of tasks to ensure that the identified path is indeed the longest path with no slack.
8. **Monitor and Update**: Throughout the project execution, monitor the critical path tasks closely as any delay in these tasks will directly impact the project completion date. Update the critical path as necessary when changes occur in the project's execution.
By following these steps, project managers can determine the critical path and focus their resources and attention on the tasks that are most critical to the project's timely completion.
All activities on a critical path have zero slack time.
True
Given the following network with activities and times estimated in days, 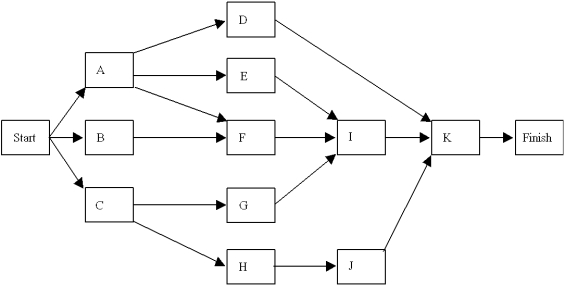 Most Activity Optimistic Probable Pessimistic A 2 5 6 B 1 3 7 C 6 7 10 D 5 12 14 E 3 4 5 F 8 9 12 G 4 6 8 H 3 6 8 I 5 7 12 J 12 13 14 K 1 3 4
a.What are the critical path activities?
b.What is the expected time to complete the project?
c.What is the probability the project will take more than 28 days to complete?
Most Activity Optimistic Probable Pessimistic A 2 5 6 B 1 3 7 C 6 7 10 D 5 12 14 E 3 4 5 F 8 9 12 G 4 6 8 H 3 6 8 I 5 7 12 J 12 13 14 K 1 3 4
a.What are the critical path activities?
b.What is the expected time to complete the project?
c.What is the probability the project will take more than 28 days to complete?
Explain how and why all predecessor activities must be considered when finding the earliest start time.
The earliest start time for an activity is equal to the smallest of the earliest finish times for all its immediate predecessors.
The linear programming model for crashing presented in the textbook assumes that any portion of the activity crash time can be achieved for a corresponding portion of the activity crashing cost.
Why should projects be monitored after the critical path is found?
The normal distribution tends to be a better approximation of the distribution of total time for shorter projects where the critical path has relatively few activities.
Which is not a significant challenge of project scheduling?
Crashing refers to an unanticipated delay in a critical path activity that causes the total time to exceed its limit.
Which of the following is a general rule for crashing activities?
Which of the following is always true about a critical activity?
The critical path for this network is A - E - F and the project completion time is 22 weeks. 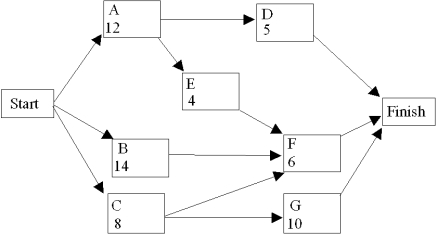 Activity Normal Time Crash Time Normal Cost Crash Cost A 12 8 8,000 12,000 B 14 10 5,000 7,500 C 8 8 10,000 10,000 D 5 3 6,000 8,000 E 4 3 5,000 7,000 F 6 5 9,000 12,000 G 10 8 5,000 8,000 If a deadline of 17 weeks is imposed,give the linear programming model for the crashing decision.
Activity Normal Time Crash Time Normal Cost Crash Cost A 12 8 8,000 12,000 B 14 10 5,000 7,500 C 8 8 10,000 10,000 D 5 3 6,000 8,000 E 4 3 5,000 7,000 F 6 5 9,000 12,000 G 10 8 5,000 8,000 If a deadline of 17 weeks is imposed,give the linear programming model for the crashing decision.
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)