Question 1

All entries in a row of a matrix of transition probabilities sum to 1.

Accepted Answer

A) True 
 B)False  True

Question 2

Precision Craft,Inc.manufactures ornate pedestal sinks.On any day,the status of a given sink is either: a)somewhere in the normal manufacturing process,b)being reworked because of a detected flaw,c)finished successfully,or d)scrapped because a flaw could not be corrected.The transition matrix is:   
a. What is the probability of a sink eventually being finished if it is currently in process?
b. What is the probability of a sink eventually being scrapped if it is currently in rework?
c. What is the probability that a sink currently in rework will have a "finished" status either tomorrow or the next day? (HINT: there are three ways this can happen.)

Accepted Answer

a..868
b..281
c..3 + .03 + .2 = .53

Question 3

Joe Isley,the owner of Big I HiFi,believes that the store's inventory can be modeled as a Markov process.If items are either classified as in stock,out of stock,discontinued from stock or put on clearance sale,then the following transition matrix has been estimated: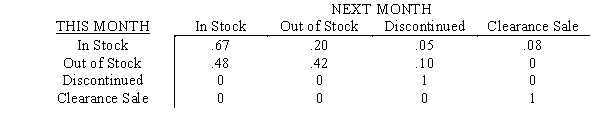   
a. Rewrite the transition matrix for the problem in the form of I, O, R, and Q submatrices.
b. Compute the fundamental matrix for this problem.
c. What is the probability of an item currently in stock being out of stock in two months?
d. What is the probability of an item currently out of stock eventually being discontinued from stock?

Accepted Answer

a.Rearranging the states gives: Note, R = $$\left[ \begin{array} { r r } .05 & .08 \ .10 & 0 \end{array} \right]$$ and Q = $$\left[ \begin{array} { c c } .67 & .20 \ .48 & .42 \end{array} \right]$$ b.N = (I F1F1F1S1F1F1F10 Q)^-1 = $$\left[ \begin{array} { r r } .33 & - .20 \ - .48 & .58 \end{array} \right] ^ { - 1 }$$ To compute (I F1F1F1S1F1F1F10 Q)^-1,first calculate its determinant, d = a₁₁a₂₂ - a₂₁a₁₂ = (.33)(.58)F1F1F1S1F1F1F10 (-.48)(-.20)= .0954 Then, N = $$\left[ \begin{array} { c c } .58 / .0954 & .20 / .0954 \ .48 / .0954 & .33 / .0954 \end{array} \right]$$ = $$\left[ \begin{array} { l l } 6.08 & 2.10 \ 5.03 & 3.46 \end{array} \right]$$ c.The tree diagram is: Therefore,the probability of an item currently in stock being out of stock in two months is .13 + .08 = .21. d.The probability of eventually moving into each of the absorbing states from the nonabsorbing states is given by: NR = $$\left[ \begin{array} { l l } 6.08 & 2.10 \ 5.03 & 3.46 \end{array} \right]$$ x $$\left[ \begin{array} { r r } .05 & .08 \ .10 & 0 \end{array} \right]$$ Discontinued Clearance Sale NR = $$\begin{array} { c } \text { In Stock } \ \text { Out of Stock } \end{array} \left[ \begin{array} { c c } .51 & .49 \ .60 & .40 \end{array} \right]$$ Hence,the probability of an item currently out of stock eventually being discontinued is .60.

Question 4

All Markov chain transition matrices have the same number of rows as columns.

Accepted Answer

A) True 
 B)False

Question 5

At steady state

Accepted Answer

A) F1F1F1S1F1F1F101(n + 1) > F1F1F1S1F1F1F101(n) 
B) F1F1F1S1F1F1F101 = F1F1F1S1F1F1F102 
C) F1F1F1S1F1F1F101 + F1F1F1S1F1F1F102 F1F1F1S1F1F1F10 1 
D) F1F1F1S1F1F1F101(n + 1) = F1F1F1S1F1F1F101 
A) F1F1F1S1F1F1F101(n + 1) > F1F1F1S1F1F1F101(n) 
B) F1F1F1S1F1F1F101 = F1F1F1S1F1F1F102 
C) F1F1F1S1F1F1F101 + F1F1F1S1F1F1F102 F1F1F1S1F1F1F10 1 
D) F1F1F1S1F1F1F101(n + 1) = F1F1F1S1F1F1F101

Question 6

The probability that the system is in state 2 in the 5th period is F1F1F1S1F1F1F105(2).

Accepted Answer

A) True 
 B)False

Question 7

For Markov processes having the memoryless property,the prior states of the system must be considered in order to predict the future behavior of the system.

Accepted Answer

A) True 
 B)False

Question 8

State j is an absorbing state if pij = 1.

Accepted Answer

A) True 
 B)False

Question 9

A recent study done by an economist for the Small Business Administration investigated failures of small business.Failures were either classified as due to poor financing,poor management,or a poor product.The failure rates differed for new businesses (under one year old)versus established businesses (over one year old.)
As the result of the economist's study,the following probabilities were determined.For new businesses the probability of failure due to financing was .15,due to management .20,and due to product .05.The corresponding probabilities for established businesses were .10,.06,and .03 respectively.
a.Determine a five-state Markov Chain transition matrix with states for new, established, and each of the three failure states. Write it in the form of I, O, R, and Q submatrices.
b.Determine the probability that a new business will survive during the next three years.
c.What proportion of new businesses eventually fail due to:(1) poor financing? (2) poor management? (3) poor product?

Accepted Answer

a. @#IMG-DLM& b..394

Question 10

The matrix of transition probabilities below deals with brand loyalty to Bark Bits and Canine Chow dog food. $$\begin{array} { c | c c } 
\text { Current } &  { \text { Next Purchase } } \
\text { Purchase } & \text { Bark Bits } & \text { Canine Chow } \
\hline \text { Bark Bits } & .75 & .25 \
\text { Canine Chow } & .20 & .80
\end{array}$$ 
a.What are the steady state probabilities?
b.What is the probability that a customer will switch brands on the next purchase after a large number of periods?

Accepted Answer

a.(F1F1F1S1F1F1F10₁ F1F1F1S1F

Question 11

Give two examples of how Markov analysis can aid decision making.

Accepted Answer

Markov analysis is a statistical techniq

Question 12

If a Markov chain has at least one absorbing state,steady-state probabilities cannot be calculated.

Accepted Answer

A) True 
 B)False

Question 13

Southside College has modeled its student loan program as a Markov process.Each year a student with a prior loan borrows again,defers repayment for a year,makes payments,pays the loan balance in full,or defaults on repayment.The transition matrix is as follows: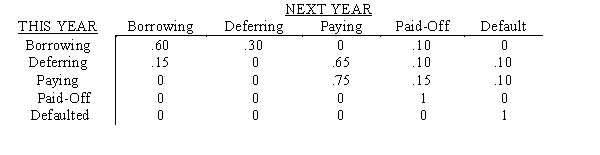   
a. If currently a student is making payments on his/her loan, what is the probability the loan will be paid in full eventually?
b. Is the probability of eventually defaulting greater for a student who is currently borrowing more or a student who is making payments?
c. What is the probability a student who is borrowing this year will repay the loan balance in full in two years or less?

Accepted Answer

a..6
b...0

Question 14

A unique matrix of transition probabilities should be developed for each customer.

Accepted Answer

A) True 
 B)False

Question 15

Transition probabilities are conditional probabilities.

Accepted Answer

A) True 
 B)False

Question 16

Markov processes use historical probabilities.

Accepted Answer

A) True 
 B)False

Question 17

In Markov analysis,we are concerned with the probability that the

Accepted Answer

A) state is part of a system. 
B) system is in a particular state at a given time. 
C) time has reached a steady state. 
D) transition will occur. 
A) state is part of a system. 
B) system is in a particular state at a given time. 
C) time has reached a steady state. 
D) transition will occur.

Question 18

The fundamental matrix is used to calculate the probability of the process moving into each absorbing state.

Accepted Answer

A) True 
 B)False

Question 19

Accounts receivable have been grouped into the following states:
State 1: Paid
State 2: Bad debt
State 3: 0-30 days old
State 4: 31-60 days old
Sixty percent of all new bills are paid before they are 30 days old.The remainder of these go to state 4.Seventy percent of all 30 day old bills are paid before they become 60 days old.If not paid,they are permanently classified as bad debts.
a.Set up the one month Markov transition matrix.
b.What is the probability that an account in state 3 will be paid?

Accepted Answer

a. @#IMG-DLM& b.NR = @#IMG-DLM& So,the p

Question 20

Appointments in a medical office are scheduled every 15 minutes.Throughout the day,appointments will be running on time or late,depending on the previous appointment only,according to the following matrix of transition probabilities: $$\begin{array} { c | c c } 
\text { Previous } &{ \text { Next Appointment } } \
\text { Appointment } & \text { On Time } & \text { Late } \
\hline \text { On Time } & .75 & .25 \
\text { Late } & .30 & .70
\end{array}$$ 
a.The day begins with the first appointment on time. What are the state probabilities for periods 1, 2, 3 and 4?
b.What are the steady state probabilities?

Accepted Answer

a.F1F1F1S1F1F1F10(0)= (1,0)
F1F1F1S1F1

All entries in a row of a matrix of transition probabilities sum to 1.

All Markov chain transition matrices have the same number of rows as columns.

At steady state

The probability that the system is in state 2 in the 5th period is ₅(2).

For Markov processes having the memoryless property,the prior states of the system must be considered in order to predict the future behavior of the system.

State j is an absorbing state if p_ij = 1.

Give two examples of how Markov analysis can aid decision making.

If a Markov chain has at least one absorbing state,steady-state probabilities cannot be calculated.

A unique matrix of transition probabilities should be developed for each customer.

Transition probabilities are conditional probabilities.

Markov processes use historical probabilities.

In Markov analysis,we are concerned with the probability that the

The fundamental matrix is used to calculate the probability of the process moving into each absorbing state.

Introduction

Introduction to Probability

Probability Distributions

Decision Analysis

Utility and Game Theory

Times Series Analysis and Forecasting

Introduction to Linear Programming

Linear Programming: Sensitivity Analysis and Interpretation of Solution

Linear Programming Applications in Marketing, Finance, and Operations Management

Distribution and Network Models

Integer Linear Programming

Advanced Optimization Applications

Project Scheduling: Pertcpm

Inventory Models

Waiting Line Models

Simulation

Filters

Exam 17: Markov Processes

All entries in a row of a matrix of transition probabilities sum to 1.

All Markov chain transition matrices have the same number of rows as columns.

At steady state

The probability that the system is in state 2 in the 5th period is 5(2).

For Markov processes having the memoryless property,the prior states of the system must be considered in order to predict the future behavior of the system.

State j is an absorbing state if pij = 1.

Give two examples of how Markov analysis can aid decision making.

If a Markov chain has at least one absorbing state,steady-state probabilities cannot be calculated.

A unique matrix of transition probabilities should be developed for each customer.

Transition probabilities are conditional probabilities.

Markov processes use historical probabilities.

In Markov analysis,we are concerned with the probability that the

The fundamental matrix is used to calculate the probability of the process moving into each absorbing state.

Introduction

Introduction to Probability

Probability Distributions

Decision Analysis

Utility and Game Theory

Times Series Analysis and Forecasting

Introduction to Linear Programming

Linear Programming: Sensitivity Analysis and Interpretation of Solution

Linear Programming Applications in Marketing, Finance, and Operations Management

Distribution and Network Models

Integer Linear Programming

Advanced Optimization Applications

Project Scheduling: Pertcpm

Inventory Models

Waiting Line Models

Simulation

Filters

The probability that the system is in state 2 in the 5th period is ₅(2).

State j is an absorbing state if p_ij = 1.