Exam 4: Introduction to Probability

The counting rule that is used for counting the number of experimental outcomes when n objects are selected from a set of N objects where order of selection is not important is called

(Multiple Choice)

4.9/5

(38)

Question 101

If P(A)= 0.62,P(B)= 0.47,and P(A $\cup$ B)= 0.88,then P(A $\cap$ B)=

(Multiple Choice)

4.9/5

(37)

Question 102

An experiment consists of selecting a student body president,vice president,and a treasurer.All undergraduate students,freshmen through seniors,are eligible for the offices.How many sample points (possible outcomes as to the classifications)exist?

(Multiple Choice)

4.8/5

(31)

Question 103

Three applications for admission to a local university are checked,and it is determined whether each applicant is male or female.The number of sample points in this experiment is

(Multiple Choice)

4.7/5

(20)

Question 104

Assume that each year the IRS randomly audits 10% of the tax returns.If a married couple has filed separate returns, a.What is the probability that both the husband and the wife will be audited? b.What is the probability that only one of them will be audited? c.What is the probability that neither one of them will be audited? d.What is the probability that at least one of them will be audited?

(Essay)

4.8/5

(33)

Question 105

In a random sample of UTC students 50% indicated they are business majors,40% engineering majors,and 10% other majors.Of the business majors,60% were females;whereas,30% of engineering majors were females.Finally,20% of the other majors were female. a.What percentage of students in this sample was female? b.Given that a person is female,what is the probability that she is an engineering major?

(Essay)

4.9/5

(28)

Question 106

From a group of three finalists for a privately endowed scholarship,two individuals are to be selected for the first and second places.Determine the number of possible selections.

(Essay)

5.0/5

(28)

Question 107

Tammy is a general contractor and has submitted two bids for two projects (A and B).The probability of getting project A is 0.65.The probability of getting project B is 0.77.The probability of getting at least one of the projects is 0.90. a.What is the probability that she will get both projects? b.Are the events of getting the two projects mutually exclusive? Explain,using probabilities. c.Are the two events independent? Explain,using probabilities.

(Essay)

4.8/5

(33)

Question 108

The probability assigned to each experimental outcome must be

(Multiple Choice)

4.8/5

(22)

Question 109

The union of two events with nonzero probabilities

(Multiple Choice)

4.8/5

(42)

Question 110

A survey of a sample of business students resulted in the following information regarding the genders of the individuals and their selected major. Selected Major 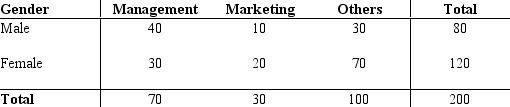a.What is the probability of selecting an individual who is majoring in Marketing? b.What is the probability of selecting an individual who is majoring in Management,given that the person is female? c.Given that a person is male,what is the probability that he is majoring in Management? d.What is the probability of selecting a male individual?

(Essay)

4.8/5

(36)

Question 111

The set of all possible outcomes of an experiment is

(Multiple Choice)

4.9/5

(34)

Question 112

When the results of experimentation or historical data are used to assign probability values,the method used to assign probabilities is referred to as the

(Multiple Choice)

4.8/5

(27)

Question 113

If P(A)= 0.50,P(B)= 0.60,and P(A $\cap$ B)= 0.30,then events A and B are

(Multiple Choice)

4.8/5

(40)

Question 114

Assume that in your hand you hold an ordinary six-sided die and a dime.You toss both the die and the dime on a table. a.What is the probability that a head appears on the dime and a six on the die? b.What is the probability that a tail appears on the dime and any number more than 3 on the die? c.What is the probability that a number larger than 2 appears on the die?

(Essay)

4.9/5

(45)

Question 115

If a penny is tossed three times and comes up heads all three times,the probability of heads on the fourth trial is

(Multiple Choice)

4.9/5

(39)

Question 116

The sample space refers to

(Multiple Choice)

4.8/5

(35)

Question 117

If A and B are independent events with P(A)= 0.65 and P(A $\cup$ B)= 0.26,then,P(B)=

(Multiple Choice)

4.8/5

(41)

Question 118

You are applying for graduate school at University A.In the past 42% of the applicants to this university have been accepted.It is also known that 70% of those students who have been accepted have had GMAT scores in excess of 550 while 40% of the students who were not accepted had GMAT scores in excess of 550.You take the GMAT exam and score 640.What is the probability that you will be accepted into graduate school of university A?

(Essay)

4.9/5

(31)

Question 119

Assume two events A and B are mutually exclusive and,furthermore,P(A)= 0.2 and P(B)= 0.4. a.Find P(A $\cap$ B). b.Find P(A $\cup$ B). c.Find P(A | B).

(Essay)

4.7/5

(28)

Question 120

Showing 101 - 120 of 138

The counting rule that is used for counting the number of experimental outcomes when n objects are selected from a set of N objects where order of selection is not important is called

If P(A)= 0.62,P(B)= 0.47,and P(A $\cup$ B)= 0.88,then P(A $\cap$ B)=

An experiment consists of selecting a student body president,vice president,and a treasurer.All undergraduate students,freshmen through seniors,are eligible for the offices.How many sample points (possible outcomes as to the classifications)exist?

Three applications for admission to a local university are checked,and it is determined whether each applicant is male or female.The number of sample points in this experiment is

From a group of three finalists for a privately endowed scholarship,two individuals are to be selected for the first and second places.Determine the number of possible selections.

The probability assigned to each experimental outcome must be

The union of two events with nonzero probabilities

The set of all possible outcomes of an experiment is

When the results of experimentation or historical data are used to assign probability values,the method used to assign probabilities is referred to as the

If P(A)= 0.50,P(B)= 0.60,and P(A $\cap$ B)= 0.30,then events A and B are

If a penny is tossed three times and comes up heads all three times,the probability of heads on the fourth trial is

The sample space refers to

If A and B are independent events with P(A)= 0.65 and P(A $\cup$ B)= 0.26,then,P(B)=

Assume two events A and B are mutually exclusive and,furthermore,P(A)= 0.2 and P(B)= 0.4. a.Find P(A $\cap$ B). b.Find P(A $\cup$ B). c.Find P(A | B).

Data and Statistics

Descriptive Statistics: Tabular and Graphical Presentations

Descriptive Statistics: Numerical Measures

Discrete Probability Distributions

Continuous Probability Distributions

Sampling and Sampling Distributions

Interval Estimation

Hypothesis Tests

Statistical Inference About Means and Proportions With Two Populations

Inferences About Population Variances

Tests of Goodness of Fit and Independence

Analysis of Variance and Experimental Design

Simple Linear Regression

Multiple Regression

Regression Analysis: Model Building

Index Numbers

Forecasting

Nonparametric Methods

Statistical Methods for Quality Control

Decision Analysis

Sample Survey

Filters

Exam 4: Introduction to Probability

The counting rule that is used for counting the number of experimental outcomes when n objects are selected from a set of N objects where order of selection is not important is called

If P(A)= 0.62,P(B)= 0.47,and P(A ∪\cup∪ B)= 0.88,then P(A ∩\cap∩ B)=

An experiment consists of selecting a student body president,vice president,and a treasurer.All undergraduate students,freshmen through seniors,are eligible for the offices.How many sample points (possible outcomes as to the classifications)exist?

Three applications for admission to a local university are checked,and it is determined whether each applicant is male or female.The number of sample points in this experiment is

From a group of three finalists for a privately endowed scholarship,two individuals are to be selected for the first and second places.Determine the number of possible selections.

The probability assigned to each experimental outcome must be

The union of two events with nonzero probabilities

The set of all possible outcomes of an experiment is

When the results of experimentation or historical data are used to assign probability values,the method used to assign probabilities is referred to as the

If P(A)= 0.50,P(B)= 0.60,and P(A ∩\cap∩ B)= 0.30,then events A and B are

If a penny is tossed three times and comes up heads all three times,the probability of heads on the fourth trial is

The sample space refers to

If A and B are independent events with P(A)= 0.65 and P(A ∪\cup∪ B)= 0.26,then,P(B)=

Assume two events A and B are mutually exclusive and,furthermore,P(A)= 0.2 and P(B)= 0.4. a.Find P(A ∩\cap∩ B). b.Find P(A ∪\cup∪ B). c.Find P(A | B).

Data and Statistics

Descriptive Statistics: Tabular and Graphical Presentations

Descriptive Statistics: Numerical Measures

Discrete Probability Distributions

Continuous Probability Distributions

Sampling and Sampling Distributions

Interval Estimation

Hypothesis Tests

Statistical Inference About Means and Proportions With Two Populations

Inferences About Population Variances

Tests of Goodness of Fit and Independence

Analysis of Variance and Experimental Design

Simple Linear Regression

Multiple Regression

Regression Analysis: Model Building

Index Numbers

Forecasting

Nonparametric Methods

Statistical Methods for Quality Control

Decision Analysis

Sample Survey

Filters

If P(A)= 0.62,P(B)= 0.47,and P(A $\cup$ B)= 0.88,then P(A $\cap$ B)=

If P(A)= 0.50,P(B)= 0.60,and P(A $\cap$ B)= 0.30,then events A and B are

If A and B are independent events with P(A)= 0.65 and P(A $\cup$ B)= 0.26,then,P(B)=

Assume two events A and B are mutually exclusive and,furthermore,P(A)= 0.2 and P(B)= 0.4. a.Find P(A $\cap$ B). b.Find P(A $\cup$ B). c.Find P(A | B).