Exam 6: Linear Regression With Multiple Regressors

When there are omitted variables in the regression, which are determinants of the dependent variable, then

Omitted variable bias

(Requires Statistics background beyond Chapters 2 and 3)One way to establish whether or not there is independence between two or more variables is to perform a $X ^ { 2 }$ - test on independence between two variables. Explain why multiple regression analysis is a preferable tool to seek a relationship between variables.

The OLS residuals in the multiple regression model

In a two regressor regression model, if you exclude one of the relevant variables then

(Requires Calculus)For the simple linear regression model of Chapter 4, $Y _ { i } = \beta _ { 0 } + \beta _ { 1 } X _ { i } + u _ { i }$ , the OLS estimator for the intercept was $\hat { \beta } _ { 0 } = \bar { Y } - \hat { \beta } _ { 1 } \bar { X }$ , and $\hat { \beta } _ { 1 } = \frac { \sum _ { i = 1 } ^ { n } X _ { i } Y _ { i } - n \overline { X Y } } { \sum _ { i = 1 } ^ { n } X _ { i } ^ { 2 } - n \bar { X } ^ { 2 } }$ Intuitively, the OLS estimators for the regression model $Y _ { i } = \beta _ { 0 } + \beta _ { 1 } X _ { 1 i } + \beta _ { 2 } X _ { 2 i } + u _ { i }$ might be $\hat { \beta } _ { 0 } = \bar { Y } - \hat { \beta } _ { 1 } \bar { X } _ { 1 } - \hat { \beta } _ { 2 } \bar { X } _ { 2 } , \hat { \beta } _ { 1 } = \frac { \sum _ { i = 1 } ^ { n } \bar { X } _ { 1i } Y _ { i } - n \bar { X } _ { 1 } \bar { Y } } { \sum _ { i = 1 } ^ { n } \bar { X } _ { 1 i } ^ { 2 } - n \bar { X } _ { 1 } ^ { 2 } }$ and $\hat { \beta } _ { 2 } = \frac { \sum _ { i = 1 } ^ { n } \bar { X } _ { 2 i } Y _ { i } - n \bar { X } _ { 2 } \bar { Y } } { \sum _ { i = 1 } ^ { n } \bar { X } _ { 2 i } ^ { 2 } - n \bar { X } _ { 2 } ^ { 2 } }$ By minimizing the prediction mistakes of the regression model with two explanatory variables, show that this cannot be the case.

The cost of attending your college has once again gone up. Although you have been told that education is investment in human capital, which carries a return of roughly 10% a year, you (and your parents)are not pleased. One of the administrators at your university/college does not make the situation better by telling you that you pay more because the reputation of your institution is better than that of others. To investigate this hypothesis, you collect data randomly for 100 national universities and liberal arts colleges from the 2000-2001 U.S. News and World Report annual rankings. Next you perform the following regression $\widehat {\operatorname { Cost}}$ = 7,311.17 + 3,985.20 × Reputation - 0.20 × Size + 8,406.79 × Dpriv - 416.38 × Dlibart - 2,376.51 × Dreligion R²=0.72, SER = 3,773.35 where Cost is Tuition, Fees, Room and Board in dollars, Reputation is the index used in U.S. News and World Report (based on a survey of university presidents and chief academic officers), which ranges from 1 ("marginal")to 5 ("distinguished"), Size is the number of undergraduate students, and Dpriv, Dlibart, and Dreligion are binary variables indicating whether the institution is private, a liberal arts college, and has a religious affiliation. (a)Interpret the results. Do the coefficients have the expected sign? (b)What is the forecasted cost for a liberal arts college, which has no religious affiliation, a size of 1,500 students and a reputation level of 4.5? (All liberal arts colleges are private.) (c)To save money, you are willing to switch from a private university to a public university, which has a ranking of 0.5 less and 10,000 more students. What is the effect on your cost? Is it substantial? (d)Eliminating the Size and Dlibart variables from your regression, the estimation regression becomes $\widehat {\operatorname { Cost}}$ = 5,450.35 + 3,538.84 × Reputation + 10,935.70 × Dpriv - 2,783.31 × Dreligion; $R ^ { 2 }$ =0.72, SER = 3,792.68 Why do you think that the effect of attending a private institution has increased now? (e)What can you say about causation in the above relationship? Is it possible that Cost affects Reputation rather than the other way around?

Consider the multiple regression model with two regressors X₁ and X₂, where both variables are determinants of the dependent variable. When omitting X₂ from the regression, then there will be omitted variable bias for $\widehat { \beta 1 }$

(Requires some Calculus)Consider the sample regression function . $Y _ { i } = \hat { \beta } _ { 0 } + \hat { \beta } _ { 1 } X _ { 1 i } + \hat { \beta } _ { 2 } X _ { 2 i }$ Take the total derivative. Next show that the partial derivative $\frac { \Delta Y _ { i } } { \Delta X _ { 1 i } }$ is obtained by holding $X _ { 2 i }$ constant, or controlling for $X _ { 2 i }$

Imperfect multicollinearity

(Requires Calculus)For the case of the multiple regression problem with two explanatory variables, derive the OLS estimator for the intercept and the two slopes.

In a multiple regression framework, the slope coefficient on the regressor X_2i

One of the least squares assumptions in the multiple regression model is that you have random variables which are "i.i.d." This stands for

The population multiple regression model when there are two regressors, X_1i and X_2i can be written as follows, with the exception of:

In the multiple regression with two explanatory variables, show that the TSS can still be decomposed into the ESS and the RSS.

A subsample from the Current Population Survey is taken, on weekly earnings of individuals, their age, and their gender. You have read in the news that women make 70 cents to the $1 that men earn. To test this hypothesis, you first regress earnings on a constant and a binary variable, which takes on a value of 1 for females and is 0 otherwise. The results were: $\widehat { E a m }$ = 570.70 - 170.72 × Female, $R ^ { 2 }$ =0.084, SER = 282.12. (a)There are 850 females in your sample and 894 males. What are the mean earnings of males and females in this sample? What is the percentage of average female income to male income? (b)You decide to control for age (in years)in your regression results because older people, up to a point, earn more on average than younger people. This regression output is as follows: $\widehat { E a m }$ = 323.70 - 169.78 × Female + 5.15 × Age, $R ^ { 2 }$ =0.135, SER = 274.45. Interpret these results carefully. How much, on average, does a 40-year-old female make per year in your sample? What about a 20-year-old male? Does this represent stronger evidence of discrimination against females?

When you have an omitted variable problem, the assumption that E(u_i X_i)= 0 is violated. This implies that

If you had a two regressor regression model, then omitting one variable which is relevant

You have collected data from Major League Baseball (MLB)to find the determinants of winning. You have a general idea that both good pitching and strong hitting are needed to do well. However, you do not know how much each of these contributes separately. To investigate this problem, you collect data for all MLB during 1999 season. Your strategy is to first regress the winning percentage on pitching quality ("Team ERA"), second to regress the same variable on some measure of hitting ("OPS - On-base Plus Slugging percentage"), and third to regress the winning percentage on both. Summary of the Distribution of Winning Percentage, On Base plus Slugging Percentage, and Team Earned Run Average for MLB in 1999 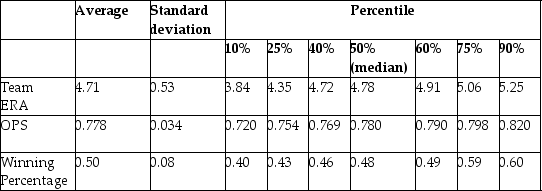The results are as follows: $\widehat {\text { Winpct }}$ = 0.94 - 0.100 × teamera, $R ^ { 2 }$ = 0.49, SER = 0.06. $\widehat {\text { Winpct }}$ = -0.68 + 1.513 × ops, $R ^ { 2 }$ =0.45, SER = 0.06. $\widehat {\text { Winpct }}$ = -0.19 - 0.099 × teamera + 1.490 × ops, $R ^ { 2 }$ =0.92, SER = 0.02. (a)Interpret the multiple regression. What is the effect of a one point increase in team ERA? Given that the Atlanta Braves had the most wins that year, wining 103 games out of 162, do you find this effect important? Next analyze the importance and statistical significance for the OPS coefficient. (The Minnesota Twins had the minimum OPS of 0.712, while the Texas Rangers had the maximum with 0.840.)Since the intercept is negative, and since winning percentages must lie between zero and one, should you rerun the regression through the origin? (b)What are some of the omitted variables in your analysis? Are they likely to affect the coefficient on Team ERA and OPS given the size of the $R ^ { 2 }$ and their potential correlation with the included variables?

You have to worry about perfect multicollinearity in the multiple regression model because