Exam 5: Utility and Game Theory

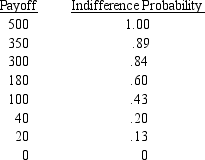
Determine decision strategies based on expected value and on expected utility for this decision tree.Use the utility function 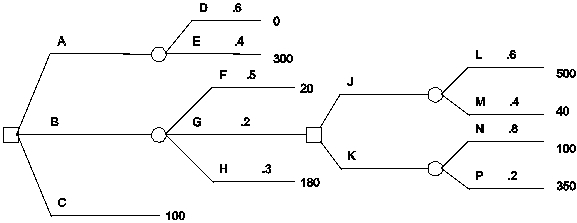seq Figure \* Arabic1

For the payoff table below,the decision maker will use P(s₁)= .15,P(s₂)= .5,and P(s₃)= .35. 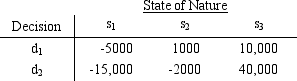a.What alternative would be chosen according to expected value? b.For a lottery having a payoff of 40,000 with probability p and -15,000 with probability (1-p),the decision maker expressed the following indifference probabilities. Let U(40,000)= 10 and U(-15,000)= 0 and find the utility value for each payoff. c.What alternative would be chosen according to expected utility?

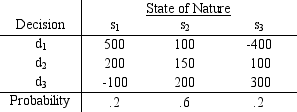
Three decision makers have assessed utilities for the problem whose payoff table appears below. 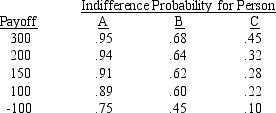a.Plot the utility function for each decision maker. b.Characterize each decision maker's attitude toward risk. c.Which decision will each person prefer?

The logic of game theory assumes that each player has different information.

Consider the following two-person zero-sum game.Assume the two players have the same three strategy options.The payoff table shows the gains for Player A. 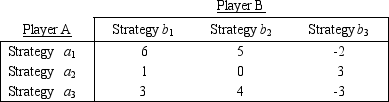Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically?

The Dollar Department Store chain has the opportunity of acquiring either 3,5,or 10 leases from the bankrupt Granite Variety Store chain.Dollar estimates the profit potential of the leases depends on the state of the economy over the next five years.There are four possible states of the economy as modeled by Dollar Department Stores and its president estimates P(s₁)= .4,P(s₂)= .3,P(s₃)= .1,and P(s₄)= .2.The utility has also been estimated.Given the payoffs (in $1,000,000's)and utility values below,which decision should Dollar make? Payoff Table State Of The Economy Over The Next 5 Years Decision s₁ s₂ s₃ s₄ d₁ -- buy 10 leases 10 5 0 -20 d₂ -- buy 5 leases 5 0 -1 -10 d₃ -- buy 3 leases 2 1 0 - 1 d₄ -- do not buy 0 0 0 0 Utility Table Payoff (in $1,000,000's)+10 +5 +2 0 -1 -10 -20 Utility +10 +5 +2 0 -1 -20 -50

With a mixed strategy,the optimal solution for each player is to randomly select among two or more of the alternative strategies.

The probability for which a decision maker cannot choose between a certain amount and a lottery based on that probability is

For a game with an optimal pure strategy,which of the following statements is false?