Exam 8: Lp Sensitivity Analysis and Interpretation of Solution

Eight of the entries have been deleted from the LINDO output that follows.Use what you know about linear programming to find values for the blanks. MIN 6 X1 + 7.5 X2 + 10 X3 SUBJECT TO 2)25 X1 + 35 X2 + 30 X3 >= 2400 3)2 X1 + 4 X2 + 8 X3 >= 400 END LP OPTIMUM FOUND AT STEP 2 OBJECTIVE FUNCTION VALUE 1)612.50000 NO.ITERATIONS= 2 RANGES IN WHICH THE BASIS IS UNCHANGED:

LINDO output is given for the following linear programming problem. MIN 12 X1 + 10 X2 + 9 X3 SUBJECT TO 2)5 X1 + 8 X2 + 5 X3 >= 60 3)8 X1 + 10 X2 + 5 X3 >= 80 END LP OPTIMUM FOUND AT STEP 1 OBJECTIVE FUNCTION VALUE 1)80.000000 NO.ITERATIONS= 1 RANGES IN WHICH THE BASIS IS UNCHANGED: a.What is the solution to the problem? b.Which constraints are binding? c.Interpret the reduced cost for x₁. d.Interpret the dual price for constraint 2. e.What would happen if the cost of x₁ dropped to 10 and the cost of x₂ increased to 12?

The amount by which an objective function coefficient would have to improve before it would be possible for the corresponding variable to assume a positive value in the optimal solution is called the

The dual price associated with a constraint is the improvement in the value of the solution per unit decrease in the right-hand side of the constraint.

The reduced cost for a positive decision variable is 0.

The amount by which an objective function coefficient can change before a different set of values for the decision variables becomes optimal is the

The 100 percent rule can be applied to changes in both objective function coefficients and right-hand sides at the same time.

The optimal solution of the linear programming problem is at the intersection of constraints 1 and 2. Max 2x₁ + x₂ s.t.4x₁ + 1x₂ < 400 4x₁ + 3x₂ < 600 1x₁ + 2x₂ $\le$ 300 x₁ ,x₂ > 0 a.Over what range can the coefficient of x₁ vary before the current solution is no longer optimal? b.Over what range can the coefficient of x₂ vary before the current solution is no longer optimal? c.Compute the dual prices for the three constraints.

Excel's Solver tool has been used in the spreadsheet below to solve a linear programming problem with a minimization objective function and all > constraints. 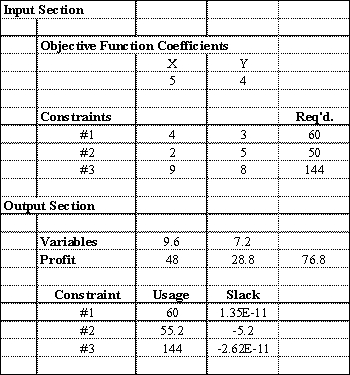a.Give the original linear programming problem. b.Give the complete optimal solution.

Any change to the objective function coefficient of a variable that is positive in the optimal solution will change the optimal solution.

Decreasing the objective function coefficient of a variable to its lower limit will create a revised problem that is unbounded.

For a minimization problem,a positive dual price indicates the value of the objective function will increase.

To solve a linear programming problem with thousands of variables and constraints

Excel's Solver tool has been used in the spreadsheet below to solve a linear programming problem with a maximization objective function and all < constraints. 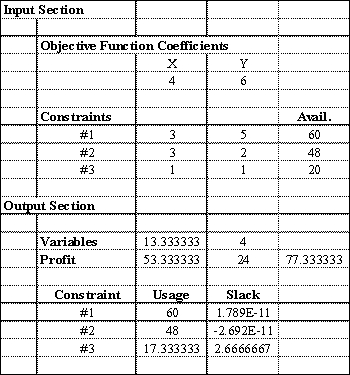a.Give the original linear programming problem. b.Give the complete optimal solution.

A negative dual price for a constraint in a minimization problem means

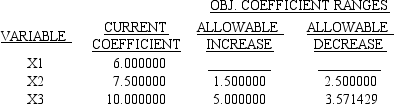
A section of output from The Management Scientist is shown here. What will happen if the right-hand-side for constraint 2 increases by 200?

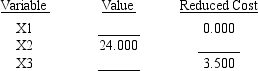
Portions of a Management Scientist output are shown below.Use what you know about the solution of linear programs to fill in the ten blanks. LINEAR PROGRAMMING PROBLEM MAX 12X1+9X2+7X3 S.T. 1)3X1+5X2+4X3<150 2)2X1+1X2+1X3<64 3)1X1+2X2+1X3<80 4)2X1+4X2+3X3>116 OPTIMAL SOLUTION Objective Function Value = 336.000 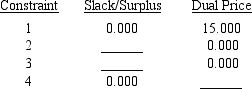OBJECTIVE COEFFICIENT RANGES RIGHT HAND SIDE RANGES

A constraint with a positive slack value

Which of the following is not a question answered by sensitivity analysis?

When the cost of a resource is sunk,then the dual price can be interpreted as the