Exam 8: Lp Sensitivity Analysis and Interpretation of Solution

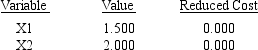
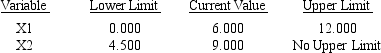Consider the following linear program: MIN 6x₁ + 9x₂ ($ cost) s.t.x₁ + 2x₂ < 8 10x₁ + 7.5x₂ > 30 x₂ > 2 x₁,x₂ > 0 The Management Scientist provided the following solution output: OPTIMAL SOLUTION Objective Function Value = 27.000 OBJECTIVE COEFFICIENT RANGES RIGHT HAND SIDE RANGES a.What is the optimal solution including the optimal value of the objective function? b.Suppose the unit cost of x₁ is decreased to $4.Is the above solution still optimal? What is the value of the objective function when this unit cost is decreased to $4? c.How much can the unit cost of x₂ be decreased without concern for the optimal solution changing? d.If simultaneously the cost of x₁ was raised to $7.5 and the cost of x₂ was reduced to $6,would the current solution still remain optimal? e.If the right-hand side of constraint 3 is increased by 1,what will be the effect on the optimal solution?

There is a dual price for every decision variable in a model.

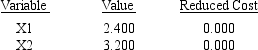
Consider the following linear program: MAX 3x₁ + 4x₂ ($ Profit) s.t.x₁ + 3x₂ < 12 2x₁ + x₂ < 8 x₁ < 3 x₁,x₂ > 0 The Management Scientist provided the following solution output: OPTIMAL SOLUTION Objective Function Value = 20.000 OBJECTIVE COEFFICIENT RANGES RIGHT HAND SIDE RANGES a.What is the optimal solution including the optimal value of the objective function? b.Suppose the profit on x₁ is increased to $7.Is the above solution still optimal? What is the value of the objective function when this unit profit is increased to $7? c.If the unit profit on x₂ was $10 instead of $4,would the optimal solution change? d.If simultaneously the profit on x₁ was raised to $5.5 and the profit on x₂ was reduced to $3,would the current solution still remain optimal?

If the dual price for the right-hand side of a < constraint is zero,there is no upper limit on its range of feasibility.

In a linear programming problem,the binding constraints for the optimal solution are 5X + 3Y < 30 2X + 5Y < 20 a.Fill in the blanks in the following sentence: As long as the slope of the objective function stays between _______ and _______,the current optimal solution point will remain optimal. b.Which of these objective functions will lead to the same optimal solution? 1)2X + 1Y 2)7X + 8Y 3)80X + 60Y 4)25X + 35Y

The dual price measures,per unit increase in the right hand side,

The binding constraints for this problem are the first and second. Min x₁ + 2x₂ s.t.x₁ + x₂ $\ge$ 300 2x₁ + x₂ $\ge$ 400 2x₁ + 5x₂ < 750 x₁ ,x₂ > 0 a.Keeping c₂ fixed at 2,over what range can c₁ vary before there is a change in the optimal solution point? b.Keeping c₁ fixed at 1,over what range can c₂ vary before there is a change in the optimal solution point? c.If the objective function becomes Min 1.5x₁ + 2x₂,what will be the optimal values of x₁,x₂,and the objective function? d.If the objective function becomes Min 7x₁ + 6x₂,what constraints will be binding? e.Find the dual price for each constraint in the original problem.

For any constraint,either its slack/surplus value must be zero or its dual price must be zero.

If the optimal value of a decision variable is zero and its reduced cost is zero,this indicates that alternative optimal solutions exist.