Exam 10: Differential Equations
Exam 1: The Derivative189 Questions
Exam 2: Applications of the Derivative93 Questions
Exam 3: Techniques of Differentiation69 Questions
Exam 4: Logarithm Functions135 Questions
Exam 5: Applications of the Exponential and Natural Logarithm Functions73 Questions
Exam 6: The Definite Integral135 Questions
Exam 7: Functions of Several Variables119 Questions
Exam 8: The Trigonometric Functions128 Questions
Exam 9: Techniques of Integration178 Questions
Exam 10: Differential Equations126 Questions
Exam 11: Taylor Polynomials and Infinite Series132 Questions
Exam 12: Probability and Calculus92 Questions
Select questions type
Consider the differential equation 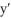 =
= 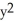 - 4y + 3. Which of the following could be a graph of solutions to this differential equation?
- 4y + 3. Which of the following could be a graph of solutions to this differential equation?
(Multiple Choice)
4.8/5  (40)
(40)
A sports enthusiast drinks 2 liters of water per hour. Water is eliminated from the body at a rate proportional to the amount of water in the body (due to perspiration). Write a differential equation satisfied by f(t), the amount of water in the body. Does this equation accurately describe this situation:
(True/False)
4.9/5  (36)
(36)
The following is a polygonal path obtained from Euler's method with n = 4 to approximate a solution f(t) of a differential equation. Indicate whether the following statements are true or false:  - (0) = 2
- (0) = 2
(True/False)
4.9/5  (44)
(44)
A cool object is to be heated to a maximum temperature M = M°C. At any time t, the rate at which the temperature rises is proportional to the difference between the actual temperature and the maximal temperature. If the object is originally 0°C, find and solve a differential equation describing this situation. Is this the solution:
(True/False)
4.8/5  (35)
(35)
Suppose the graph below gives a solution to the differential equation = g(P) where P is the price of a product and s is the weekly sales. 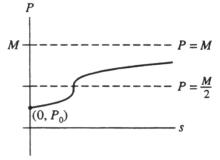 Which of the following statements is/are true?
(I) g(M) = 0
(II)
(III)
(IV) g( ) > 0
Which of the following statements is/are true?
(I) g(M) = 0
(II)
(III)
(IV) g( ) > 0
(Multiple Choice)
4.7/5  (30)
(30)
A nutritionist proposes the following model for weight loss on a program she is developing: + 0.006w = C where w(t) is a person's weight (in pounds) after t days of consuming exactly C calories per day. A person weighing 180 pounds goes on this diet program consuming 2400 calories per day. Use the above model to predict how long will it take this person to lose 15 pounds.
(Multiple Choice)
4.7/5  (33)
(33)
Solve the differential equation with the given initial condition.
-
(Multiple Choice)
5.0/5  (43)
(43)
A jug of milk at 50° is placed outdoors at a temperature of 100°. If after 5 minutes the temperature of the milk is 60°, write the equation giving the temperature of the milk as a function of time. Enter your answer exactly as:
T = a + c
(Short Answer)
4.9/5  (32)
(32)
Solve the problem.
-An initial deposit of $24,000 is made into an account that earns 5% compounded continuously. Money is then withdrawn at a constant rate of $4000 a year until the amount in the account is 0. Find the equation for the amount in the account at any time t. When is the amount 0?
(Multiple Choice)
5.0/5  (36)
(36)
Suppose that y = f(t) satisfies the differential equation = + 3y, f(0) = 2. If Euler's method with is used to construct an approximation p(t) to f(t) for 0 ≤ t ≤ 1, find p(0.1).
(Multiple Choice)
4.8/5  (36)
(36)
One or more initial conditions are given for the differential equation. Use the qualitative theory of autonomous differential equations to sketch the graphs of the corresponding solution. Include a yz-graph as well as a ty-graph. Do these graphs represent the situation? 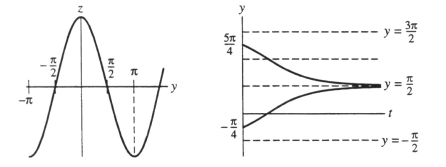
(True/False)
4.9/5  (33)
(33)
Given the differential equation with the given initial condition: is this the solution
(True/False)
4.7/5  (33)
(33)
Suppose the relationship between the price p, of a product and the weekly sales, s, of the product is given by the differential equation Then
(Multiple Choice)
4.8/5  (31)
(31)
Given the differential equation with the given initial condition: is this the solution
(True/False)
4.9/5  (44)
(44)
Find the constant solutions to the differential equation: .
Enter just one integer or two separated by a comma (no label).
(Short Answer)
4.8/5  (35)
(35)
Given = - 1. On a ty-coordinate system sketch the solutions corresponding to the initial conditions and . Does this graph represent the situation? 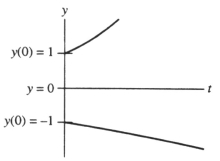
(True/False)
4.9/5  (30)
(30)
Solve the differential equation with the given initial condition.
-
(Multiple Choice)
4.8/5  (36)
(36)
Use Euler's method with n = 5 on the interval 0 ≤ t ≤ to approximate the solution f(t) to Is the following the correct answer? =0;=1 =0.1;=1.3 =0.2;=1.69 3=0.3;=2.197 =0.4;=2.8561 5=0.5; y5 =3.71293
(True/False)
4.9/5  (34)
(34)
Showing 21 - 40 of 126
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)