Exam 10: Differential Equations
Exam 1: The Derivative189 Questions
Exam 2: Applications of the Derivative93 Questions
Exam 3: Techniques of Differentiation69 Questions
Exam 4: Logarithm Functions135 Questions
Exam 5: Applications of the Exponential and Natural Logarithm Functions73 Questions
Exam 6: The Definite Integral135 Questions
Exam 7: Functions of Several Variables119 Questions
Exam 8: The Trigonometric Functions128 Questions
Exam 9: Techniques of Integration178 Questions
Exam 10: Differential Equations126 Questions
Exam 11: Taylor Polynomials and Infinite Series132 Questions
Exam 12: Probability and Calculus92 Questions
Select questions type
Which of the following is a sketch of the solution of = - 9; y(0) = 2 ?
(Multiple Choice)
4.8/5  (30)
(30)
Let f(t) be the solution of = t + y + , f(0) = 2. If Euler's method with n = 4 is used to approximate f(t) for find f .
(Multiple Choice)
4.9/5  (36)
(36)
Given the differential equation with the given initial condition: is this the solution
(True/False)
4.8/5  (30)
(30)
One or more initial conditions are given for the differential equation. Use the qualitative theory of autonomous differential equations to sketch the graphs of the corresponding solution. Include a yz-graph as well as a ty-graph. Do these graphs represent the situation? 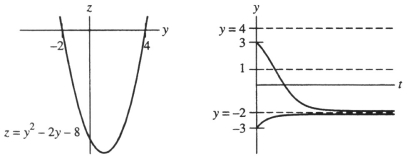
(True/False)
4.9/5  (40)
(40)
Consider the differential equation = g(y) where g(y) is the function whose graph is shown below: 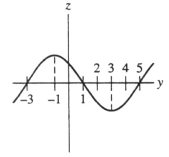 Indicate whether the following statements are true or false.
-If the initial value of y(0) is 2, then the corresponding solution has an inflection point.
Indicate whether the following statements are true or false.
-If the initial value of y(0) is 2, then the corresponding solution has an inflection point.
(True/False)
4.9/5  (36)
(36)
Consider the differential equation = g(y) where g(y) is the function whose graph is shown below:  Indicate whether the following statements are true or false.
-y = -3, y = 1, and y = 5 are the constant solutions to = g(y).
Indicate whether the following statements are true or false.
-y = -3, y = 1, and y = 5 are the constant solutions to = g(y).
(True/False)
4.7/5  (37)
(37)
Solve the differential equation with the given initial condition.
-
(Multiple Choice)
5.0/5  (44)
(44)
A savings account earns 6% annual interest, compounded continuously. An initial deposit of $8500 is made, and thereafter money is withdrawn continuously at the rate of $480 per year. Does the following accurately represent this situation:
(True/False)
4.9/5  (39)
(39)
v
-An initial deposit of $8,000 is made into an account earning 6.5% compounded continuously. Thereafter, money is deposited into the account at a constant rate of $2600 per year. Find the amount in this account at any time t. How much is in this account after 5 years?
(Multiple Choice)
4.9/5  (32)
(32)
Consider the differential equation y' = y - . Which of the following statements is/are true?
(Multiple Choice)
4.8/5  (45)
(45)
Find the integrating factor, the general solution, and the particular solution satisfying the initial condition. - 4y = -2 ; y(0) = -1
(Multiple Choice)
4.9/5  (28)
(28)
Use Euler's method with n = 2 to approximate the solution f(t) to Estimate f(1).
Enter just a reduced fraction of form .
(Short Answer)
4.8/5  (45)
(45)
A certain drug is introduced into a person's bloodstream. Suppose that the rate of decrease of the concentration of the drug in the blood is directly proportional to the product of two quantities: (a) the amount of time elapsed since the drug was introduced, and (b) the square of the concentration. Let y = f(t) denote the concentration of the drug in the blood at time t. Set up a differential equation satisfied by f(t). Does the following accurately describe this situation:
(True/False)
4.8/5  (31)
(31)
Combine the terms y and into the derivative of a product: .
Is this derivative correct: ?
(True/False)
4.9/5  (35)
(35)
Combine the terms y and into the derivative of a product, then solve the equation. . Is this the solution:
(True/False)
4.9/5  (34)
(34)
Suppose that a substance A is converted to substance B at a rate that is proportional to the cube of the amount of B present. The amount of A and B together is always constant, say M. If f( t) = y is the amount of A present at time t, then which of the following differential equation describes the situation?
(Multiple Choice)
4.7/5  (37)
(37)
Solve the initial value problem using an integrating factor.
-t + 3y = 5t; , t > 0
(Multiple Choice)
4.8/5  (33)
(33)
Solve the differential equation with the given initial condition.
-
(Multiple Choice)
4.8/5  (37)
(37)
Which of the following functions solves the differential equation:
(Multiple Choice)
4.9/5  (40)
(40)
Showing 41 - 60 of 126
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)