Exam 14: Functions of Two or More Variables
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
The following table shows the monthly mortgage payment R for a given interest rate 5% as a function of the amount financed A (in thousands of dollars) and the duration of the loan n in years. If 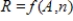 , use the table to find
, use the table to find 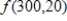 . Round your answer to the nearest cent.
. Round your answer to the nearest cent.
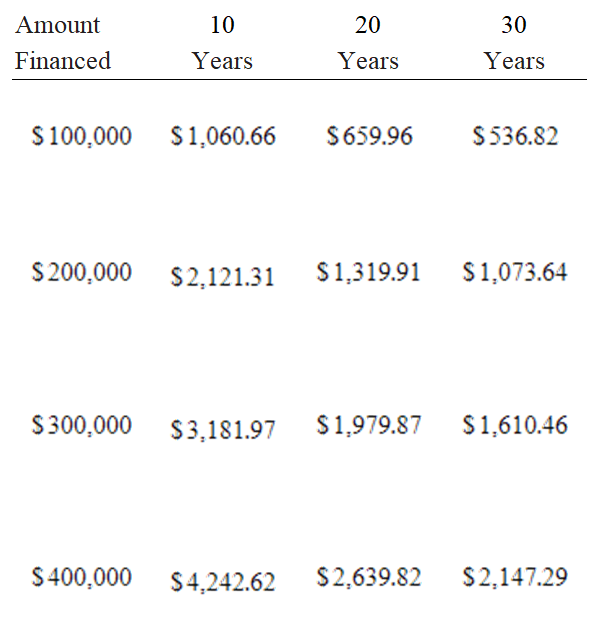
(Multiple Choice)
5.0/5  (38)
(38)
Suppose that the number of crates of an agricultural product is given by 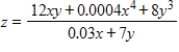 , where x is the number of hours of and y is the number of acres of the crop. Find the marginal productivity of the number of hours of labor when
, where x is the number of hours of and y is the number of acres of the crop. Find the marginal productivity of the number of hours of labor when 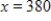 and
and 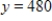 .
.
(Multiple Choice)
4.8/5  (37)
(37)
Suppose that the total cost of producing 1 unit of a product is given by 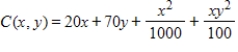 dollars, where x represents the cost per pound of raw materials and y represents the hourly rate for labor. The present cost for raw materials is $11 per pound and the present hourly rate for labor is $24. How will an increase of $1 per hour in labor costs affect the total cost? Round your answer to the nearest cent.
dollars, where x represents the cost per pound of raw materials and y represents the hourly rate for labor. The present cost for raw materials is $11 per pound and the present hourly rate for labor is $24. How will an increase of $1 per hour in labor costs affect the total cost? Round your answer to the nearest cent.
(Multiple Choice)
4.9/5  (31)
(31)
There are different models for measuring the effects of high temperature and humidity. One of these is the Summer Simmer Index (S), given by 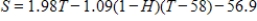 , where T is the air temperature (in degrees Fahrenheit) and H is the relative humidity (expressed as a decimal).
In a certain city, the measured temperature and humidity on a given day are:
Maximum:
, where T is the air temperature (in degrees Fahrenheit) and H is the relative humidity (expressed as a decimal).
In a certain city, the measured temperature and humidity on a given day are:
Maximum: 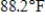 with 47% humidity
Minimum:
with 47% humidity
Minimum: 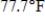 with 78% humidity
Calculate the Summer Simmer Index S for both the maximum and minimum temperatures.
with 78% humidity
Calculate the Summer Simmer Index S for both the maximum and minimum temperatures.
(Multiple Choice)
4.9/5  (36)
(36)
The total cost (in dollars) of producing 1 unit of a product is given by 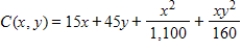 , where x represents the cost per pound of raw materials and y represents the hourly rate for labor. The present cost for raw materials is $15 per pound and the present hourly rate for labor is $11. Indicate how to use the cost function C to determine how an increase of $1 per pound for raw materials will affect the total cost. Round your answer to two decimal places.
, where x represents the cost per pound of raw materials and y represents the hourly rate for labor. The present cost for raw materials is $15 per pound and the present hourly rate for labor is $11. Indicate how to use the cost function C to determine how an increase of $1 per pound for raw materials will affect the total cost. Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (27)
(27)
Dr. Paul Siple conducted studies testing the effect of wind on the formation of ice at various temperatures and developed the concept of wind chill, which we hear reported during winter weather reports. One form of the formula that meteorologists use to calculate wind chill temperature is 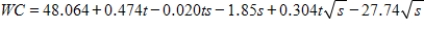 , where s is wind speed and t is the actual air temperature. Find
, where s is wind speed and t is the actual air temperature. Find 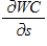 when the temperature is
when the temperature is 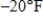 and the wind speed is 40 mph. Round your answer to two decimal places.
and the wind speed is 40 mph. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
The cost per day to society of an epidemic is 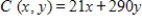 , where C is in dollars, x is the number of people infected on a given day, and y is the number of people who die on a given day. If 18,500 people are infected and 10 people die on a given day, what is the cost to society? Round your answer to the nearest dollar.
, where C is in dollars, x is the number of people infected on a given day, and y is the number of people who die on a given day. If 18,500 people are infected and 10 people die on a given day, what is the cost to society? Round your answer to the nearest dollar.
(Multiple Choice)
5.0/5  (35)
(35)
The following table gives the actual or projected population in millions for a certain city for selected years from 2000 to 2050. Use linear regression to find the linear equation that is the best fit for the data, with x equal to the number of years past 2000.
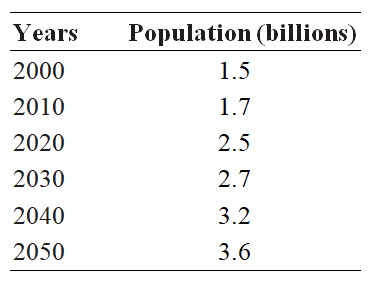
(Multiple Choice)
4.8/5  (43)
(43)
Suppose that the joint cost (in dollars) for two products is given by 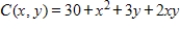 , where x represents the quantity of product X produced and y represents the quantity of product Y produced. Find and interpret the marginal cost with respect to y if 6 units of product X and 10 units of product Y are produced.
, where x represents the quantity of product X produced and y represents the quantity of product Y produced. Find and interpret the marginal cost with respect to y if 6 units of product X and 10 units of product Y are produced.
(Multiple Choice)
4.8/5  (32)
(32)
Suppose that the data in the table below shows the average earnings of year-round full-time workers by gender for several different levels of educational attainment. Find and interpret the slope of the linear regression line. Round the slope to three decimal places.
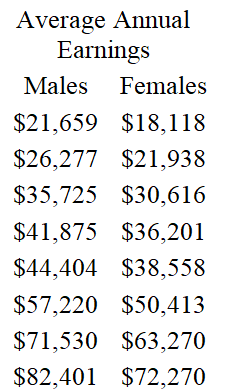
(Multiple Choice)
4.9/5  (35)
(35)
In economics, the most economical quantity Q of goods (TVs, dresses, gallons of paint, etc.) for a store to order is given by Wilson's lot size formula 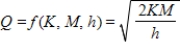 , where K is the cost of placing the order, M is the number of items sold per week, and h is the weekly holding cost for each item (the cost of storage space, utilities, taxes, security, etc.). Find
, where K is the cost of placing the order, M is the number of items sold per week, and h is the weekly holding cost for each item (the cost of storage space, utilities, taxes, security, etc.). Find 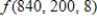 .
.
(Multiple Choice)
4.8/5  (38)
(38)
Suppose that the utility function for two goods X and Y is given by 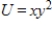 , and a consumer purchases 2 units of X and 6 units of Y. If the consumer purchases 2 units of Y, how many units of X must be purchased to retain the same level of utility?
, and a consumer purchases 2 units of X and 6 units of Y. If the consumer purchases 2 units of Y, how many units of X must be purchased to retain the same level of utility?
(Multiple Choice)
4.8/5  (34)
(34)
Showing 41 - 60 of 122
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)