Exam 18: Final Exam
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Find the directional derivative of 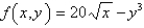 at the point (1, 3) in the direction toward the point (3, 1).
at the point (1, 3) in the direction toward the point (3, 1).
Free
(Multiple Choice)
4.7/5  (40)
(40)
Correct Answer:
B
Find a nonzero vector orthogonal to the plane through the points P, Q, and R. 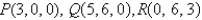
Free
(Multiple Choice)
4.8/5  (29)
(29)
Correct Answer:
C
Use implicit differentiation to find an equation of the tangent line to the curve at the given point. 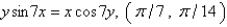
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
D
Find the average value of the function 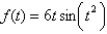 on the interval
on the interval 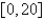 . Round your answer to 3 decimal places.
. Round your answer to 3 decimal places.
(Multiple Choice)
4.8/5  (39)
(39)
Find the area of the region that lies under the given curve. Round the answer to three decimal places. 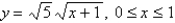
(Multiple Choice)
4.9/5  (32)
(32)
A piece of wire 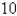 m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle. How should the wire be cut for the square so that the total area enclosed is a minimum? Round your answer to the nearest hundredth.
m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle. How should the wire be cut for the square so that the total area enclosed is a minimum? Round your answer to the nearest hundredth.
(Multiple Choice)
4.9/5  (25)
(25)
Use spherical coordinates. Evaluate 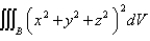 , where
, where 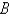 is the ball with center the origin and radius
is the ball with center the origin and radius 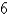 .
.
(Multiple Choice)
4.8/5  (42)
(42)
Find the volume of the resulting solid if the region under the curve 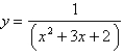 from
from 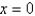 to
to 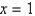 is rotated about the x-axis. Round your answer to four decimal places.
is rotated about the x-axis. Round your answer to four decimal places.
(Essay)
4.9/5  (37)
(37)
Find the volume of the given solid.
Under the paraboloid 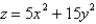 and above the rectangle
and above the rectangle 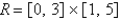 .
.
(Essay)
4.8/5  (36)
(36)
If 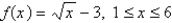 , find the Riemann sum with n = 5 correct to 3 decimal places, taking the sample points to be midpoints.
, find the Riemann sum with n = 5 correct to 3 decimal places, taking the sample points to be midpoints.
(Essay)
4.8/5  (35)
(35)
Find the area of the region that is bounded by the given curve and lies in the specified sector. 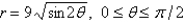
(Short Answer)
4.7/5  (36)
(36)
The acceleration function (in m / s2) and the initial velocity are given for a particle moving along a line. Find the velocity at time t and the distance traveled during the given time interval. 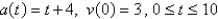
(Multiple Choice)
4.8/5  (42)
(42)
The masses 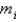 are located at the point
are located at the point 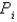 . Find the moments
. Find the moments 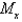 and
and 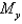 and the center of mass of the system.
and the center of mass of the system. 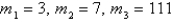 ;
; 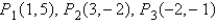
(Multiple Choice)
4.9/5  (38)
(38)
Find the volume of the given solid.
Under the paraboloid 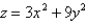 and above the rectangle
and above the rectangle 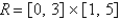 .
.
(Essay)
4.8/5  (32)
(32)
Showing 1 - 20 of 44
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)