Exam 10: Parametric Equations and Polar Coordinates
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Consider the polar equation 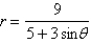 .
(a) Find the eccentricity and an equation of the directrix of the conic.
(b) Identify the conic.
(c) Sketch the curve.
.
(a) Find the eccentricity and an equation of the directrix of the conic.
(b) Identify the conic.
(c) Sketch the curve.
Free
(Essay)
4.8/5  (37)
(37)
Correct Answer:
a. 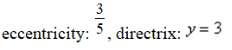
b. ellipse
c. 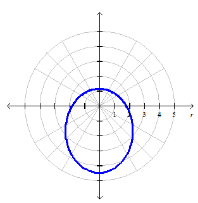
Find an equation of the hyperbola with vertices 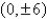 and asymptotes
and asymptotes 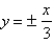 .
.
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
A
Find the surface area generated by rotating the lemniscate 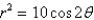 about the line
about the line 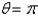 .
.
Free
(Multiple Choice)
4.8/5  (38)
(38)
Correct Answer:
B
Find an equation for the conic that satisfies the given conditions. parabola, vertex (0, 0), focus (0, - 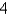 )
)
(Multiple Choice)
4.9/5  (32)
(32)
Suppose a planet is discovered that revolves around its sun in an elliptical orbit with the sun at one focus. Its perihelion distance (minimum distance from the planet to the sun) is approximately 1.3 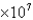 km, and its aphelion distance (maximum distance from the planet to the sun) is approximately 6.9
km, and its aphelion distance (maximum distance from the planet to the sun) is approximately 6.9 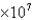 km. Approximate the eccentricity of the planet's orbit. Round to three decimal places.
km. Approximate the eccentricity of the planet's orbit. Round to three decimal places.
(Multiple Choice)
4.8/5  (36)
(36)
Write a polar equation in r and of an ellipse with the focus at the origin, with the eccentricity 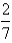 and directrix
and directrix 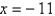 .
.
(Multiple Choice)
4.9/5  (33)
(33)
Find a Cartesian equation for the curve described by the given polar equation. 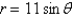
(Essay)
4.8/5  (28)
(28)
Find the area of the region that is bounded by the given curve and lies in the specified sector. 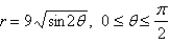
(Essay)
4.8/5  (30)
(30)
The graph of the following curve is given. Find the area that it encloses. 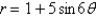
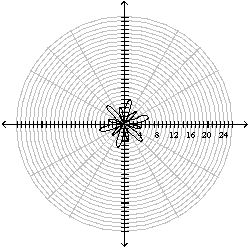
(Multiple Choice)
4.9/5  (34)
(34)
Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. 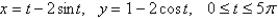
(Essay)
4.9/5  (41)
(41)
The point in a lunar orbit nearest the surface of the moon is called perilune and the point farthest from the surface is called apolune. The Apollo 11 spacecraft was placed in an elliptical lunar orbit with perilune altitude 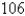 km and apolune altitude
km and apolune altitude 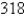 km (above the moon). Find an equation of this ellipse if the radius of the moon is
km (above the moon). Find an equation of this ellipse if the radius of the moon is 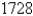 km and the center of the moon is at one focus.
km and the center of the moon is at one focus.
(Essay)
4.8/5  (40)
(40)
Using the arc length formula, set up, but do not evaluate, an integral equal to the total arc length of the ellipse. 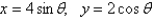
(Essay)
4.8/5  (35)
(35)
The curve 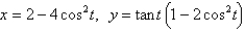 cross itself at some point
cross itself at some point 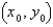 . Find the equations of both tangent lines at that point.
. Find the equations of both tangent lines at that point.
(Multiple Choice)
4.7/5  (38)
(38)
Find the area of the region that lies inside the first curve and outside the second curve. 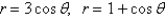
(Multiple Choice)
4.7/5  (30)
(30)
Write a polar equation in r and of an ellipse with the focus at the origin, with the eccentricity 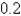 and vertex at
and vertex at 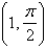 .
.
(Multiple Choice)
4.8/5  (45)
(45)
Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. 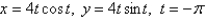
(Essay)
4.8/5  (38)
(38)
Set up, but do not evaluate, an integral that represents the length of the parametric curve. 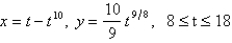
(Essay)
4.9/5  (36)
(36)
Showing 1 - 20 of 72
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)