Exam 11: Infinite Sequences and Series
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Suppose that the radius of convergence of the power series 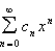 is
is 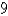 . What is the radius of convergence of the power series
. What is the radius of convergence of the power series 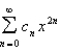 .
.
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
D
Use the binomial series to expand the function as a power series. Find the radius of convergence. 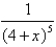
Free
(Essay)
4.8/5  (29)
(29)
Correct Answer:
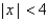
Determine whether the sequence converges or diverges. If it converges, find the limit. 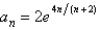
Free
(Essay)
4.8/5  (29)
(29)
Correct Answer:
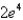
Determine whether the sequence defined by 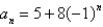 converges or diverges. If it converges, find its limit.
converges or diverges. If it converges, find its limit.
(Multiple Choice)
4.8/5  (40)
(40)
Determine whether the series is convergent or divergent by expressing 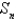 as a telescoping sum. If it is convergent, find its sum.
as a telescoping sum. If it is convergent, find its sum. 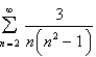 .
.
(Multiple Choice)
5.0/5  (31)
(31)
Which of the partial sums of the alternating series 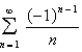 are overestimates of the total sum?
are overestimates of the total sum?
(Multiple Choice)
4.7/5  (34)
(34)
Use the Comparison Test to determine whether the series is convergent or divergent. 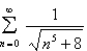
(Short Answer)
4.8/5  (39)
(39)
A rubber ball is dropped from a height of 5 m onto a flat surface. Each time the ball hits the surface, it rebounds to 50% of its previous height. Find the total distance the ball travels.
(Multiple Choice)
4.9/5  (34)
(34)
The terms of a series are defined recursively by the equations 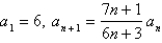 .
Determine whether
.
Determine whether 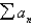 converges or diverges.
converges or diverges.
(Short Answer)
5.0/5  (41)
(41)
How many terms of the series do we need to add in order to find the sum to the indicated accuracy? 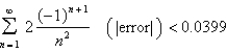
(Multiple Choice)
4.8/5  (34)
(34)
Find the radius of convergence and the interval of convergence of the power series. 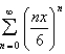
(Multiple Choice)
4.9/5  (34)
(34)
Determine whether the given series is convergent or divergent. 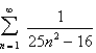
(Short Answer)
4.8/5  (34)
(34)
Determine whether the given series converges or diverges. If it converges, find its sum. 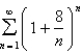
(Multiple Choice)
4.7/5  (30)
(30)
Showing 1 - 20 of 158
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)