Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution
Exam 1: Introduction53 Questions
Exam 2: An Introduction to Linear Programming56 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution44 Questions
Exam 4: Linear Programming Applications in Marketing, finance, and OM52 Questions
Exam 5: Advanced Linear Programming Applications39 Questions
Exam 6: Distribution and Network Models62 Questions
Exam 7: Integer Linear Programming52 Questions
Exam 8: Nonlinear Optimization Models45 Questions
Exam 9: Project Scheduling: Pertcpm60 Questions
Exam 10: Inventory Models60 Questions
Exam 11: Waiting Line Models56 Questions
Exam 12: Simulation53 Questions
Exam 13: Decision Analysis80 Questions
Exam 14: Multicriteria Decisions42 Questions
Exam 15: Time Series Analysis and Forecasting53 Questions
Exam 16: Markov Processes36 Questions
Exam 17: Linear Programming: Simplex Method45 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality32 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems39 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming41 Questions
Select questions type
The reduced cost of a variable is the dual value of the corresponding nonnegativity constraint.
Free
(True/False)
4.8/5  (28)
(28)
Correct Answer:
True
Excel's Solver tool has been used in the spreadsheet below to solve a linear programming problem with a minimization objective function and all ≥ constraints. 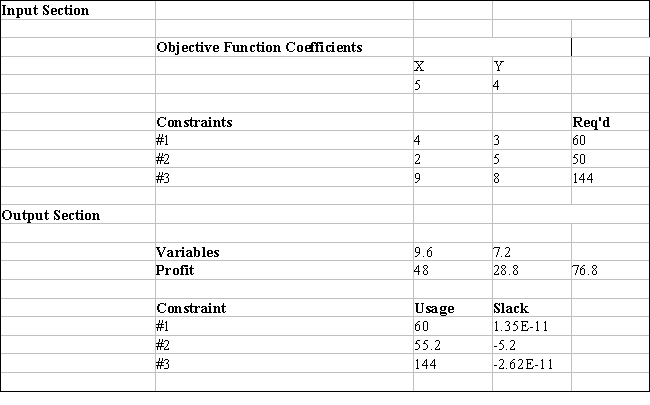
a.Give the original linear programming problem.
b.Give the complete optimal solution.
a.Give the original linear programming problem.
b.Give the complete optimal solution.
Free
(Essay)
4.8/5  (36)
(36)
Correct Answer:
The amount of a sunk cost will vary depending on the values of the decision variables.
Free
(True/False)
4.9/5  (37)
(37)
Correct Answer:
False
The amount the objective function coefficient of a decision variable would have to improve before that variable would have a positive value in the solution is the
(Multiple Choice)
4.8/5  (27)
(27)
Sensitivity analysis information in computer output is based on the assumption that
(Multiple Choice)
4.8/5  (35)
(35)
When the right-hand sides of two constraints are each increased by one unit,the objective function value will be adjusted by the sum of the constraints' dual prices.
(True/False)
4.9/5  (34)
(34)
The optimal solution of this linear programming problem is at the intersection of constraints 1 and 2. 
a.
Over what range can the coefficient of x1 vary before the current solution is no longer optimal?
b.
Over what range can the coefficient of x2 vary before the current solution is no longer optimal?
c.Compute the dual prices for the three constraints.
a.
Over what range can the coefficient of x1 vary before the current solution is no longer optimal?
b.
Over what range can the coefficient of x2 vary before the current solution is no longer optimal?
c.Compute the dual prices for the three constraints.
(Essay)
4.9/5  (31)
(31)
Consider the following linear program:  The graphical solution to the problem is shown below.From the graph,we see that the optimal solution occurs at x1 = 5,x2 = 3,and z = 46.
The graphical solution to the problem is shown below.From the graph,we see that the optimal solution occurs at x1 = 5,x2 = 3,and z = 46. 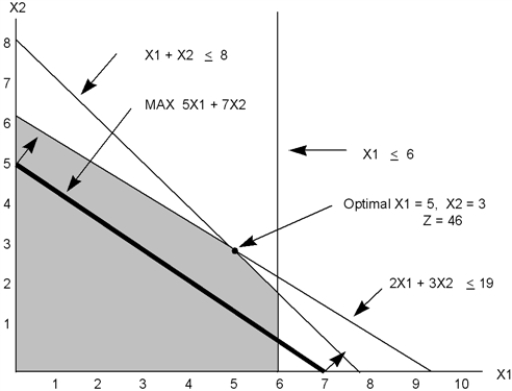 a.Calculate the range of optimality for each objective function coefficient.
b.Calculate the dual price for each resource.
a.Calculate the range of optimality for each objective function coefficient.
b.Calculate the dual price for each resource.
(Essay)
4.8/5  (39)
(39)
If the range of feasibility for b1 is between 16 and 37,then if b1 = 22,the optimal solution will not change from the original optimal solution.
(True/False)
4.8/5  (37)
(37)
If two or more objective function coefficients are changed simultaneously,further analysis is necessary to determine whether the optimal solution will change.
(True/False)
5.0/5  (34)
(34)
Relevant costs should be reflected in the objective function,but sunk costs should not.
(True/False)
4.7/5  (42)
(42)
The cost that varies depending on the values of the decision variables is a
(Multiple Choice)
4.9/5  (36)
(36)
Increasing the right-hand side of a nonbinding constraint will not cause a change in the optimal solution.
(True/False)
4.8/5  (33)
(33)
If the range of feasibility indicates that the original amount of a resource,which was 20,can increase by 5,then the amount of the resource can increase to 25.
(True/False)
4.8/5  (31)
(31)
When two or more objective function coefficients are changed simultaneously,further analysis is necessary to determine whether the optimal solution will change.
(True/False)
4.8/5  (28)
(28)
A negative dual price for a constraint in a minimization problem means
(Multiple Choice)
4.9/5  (40)
(40)
To solve a linear programming problem with thousands of variables and constraints,
(Multiple Choice)
4.7/5  (42)
(42)
A cost that is incurred no matter what values the decision variables assume is a(n)
(Multiple Choice)
4.8/5  (33)
(33)
An objective function reflects the relevant cost of labor hours used in production rather than treating them as a sunk cost.The correct interpretation of the dual price associated with the labor hours constraint is the
(Multiple Choice)
4.8/5  (31)
(31)
When the cost of a resource is sunk,then the dual price can be interpreted as the
(Multiple Choice)
4.8/5  (31)
(31)
Showing 1 - 20 of 44
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)