Exam 2: Functions
Exam 1: Fundamentals229 Questions
Exam 2: Functions98 Questions
Exam 3: Polynomial and Rational Functions145 Questions
Exam 4: Exponential and Logarithmic Functions99 Questions
Exam 5: Trigonometric Functions: Unit Circle Approach100 Questions
Exam 6: Trigonometric Functions: Right Triangle Approach119 Questions
Exam 7: Analytic Trigonometry119 Questions
Exam 8: Polar Coordinates and Parametric Equations109 Questions
Exam 9: Vectors in Two and Three Dimensions96 Questions
Exam 10: Systems of Equations and Inequalities140 Questions
Exam 11: Conic Sections99 Questions
Exam 12: Sequences and Series100 Questions
Exam 13: Limits: a Preview of Calculus66 Questions
Select questions type
Let .
(a) Sketch the graph of .
(b) Find the domain and the range of .
(Essay)
4.7/5  (31)
(31)
Determine whether the given curve is the graph of a function of . If it is, state the domain and range of the function. 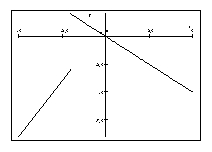
(Multiple Choice)
4.7/5  (38)
(38)
Let .
(a) Sketch the graph of .
(b) Find the domain of .
(c) State the intervals on which is increasing and on which is decreasing.
(Essay)
4.9/5  (43)
(43)
For the functions and , find , , , and their domains. Answer domain:
f-g=-=- domain: (-\infty,1)\cup(1,2)\cup(2,\infty) fg= = domain: (-\infty,1)\cup(1,2)\cup(2,\infty) = domain: (-\infty,0)\cup(0,1)\cup(1,2)\cup(2,\infty) 10.
Given and , find .
(Essay)
4.8/5  (37)
(37)
A man is running around a circular track that is 200 m in circumference. An observer uses a stopwatch to record the runner's time at the end of each lap, obtaining the data in the following table.
What was the man's average speed (rate) between 108 s and 203 s? Round the answer to two decimal places.
Time (s) Distance () 32 200 68 400 108 600 152 800 203 1000 263 1200 335 1400 412 1600
(Short Answer)
4.9/5  (36)
(36)
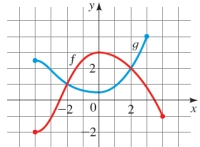
Graphs of the functions f and g are given.
(a) Which is larger,
(b) Which is larger,
(c) For which values of x is
(Essay)
4.9/5  (41)
(41)
A function is given. Use a graphing calculator to draw the graph of f. Find the domain and range of f from the graph.
(Essay)
4.9/5  (40)
(40)
A function is given.
(a) Find all the local maximum and minimum values of the function and the value of x at which each occurs.
(b) Find the intervals on which the function is increasing and on which the function is decreasing. State all answers correct to two decimal places.
(Essay)
4.8/5  (31)
(31)
Let ,
(a) Sketch the graph of
then use it to sketch the graph of
.
(b) Find
.
(Essay)
4.8/5  (36)
(36)
Showing 41 - 60 of 98
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)