Exam 2: Functions
Exam 1: Fundamentals229 Questions
Exam 2: Functions98 Questions
Exam 3: Polynomial and Rational Functions145 Questions
Exam 4: Exponential and Logarithmic Functions99 Questions
Exam 5: Trigonometric Functions: Unit Circle Approach100 Questions
Exam 6: Trigonometric Functions: Right Triangle Approach119 Questions
Exam 7: Analytic Trigonometry119 Questions
Exam 8: Polar Coordinates and Parametric Equations109 Questions
Exam 9: Vectors in Two and Three Dimensions96 Questions
Exam 10: Systems of Equations and Inequalities140 Questions
Exam 11: Conic Sections99 Questions
Exam 12: Sequences and Series100 Questions
Exam 13: Limits: a Preview of Calculus66 Questions
Select questions type
For the function determine the average rate of change between the values and
(Essay)
4.8/5  (42)
(42)
Use a graphing device to the graph of the function . State approximately the intervals on which the function is increasing and on which the function is decreasing.
(Essay)
4.8/5  (46)
(46)
Graphs of the functions f and g are given.
(a) Which is larger,
(b) Which is larger,
(c) For which values of x is
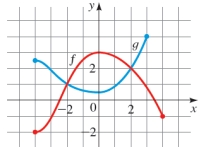
(Essay)
4.8/5  (43)
(43)
Determine whether or not the function given by the graph is one-to-one. 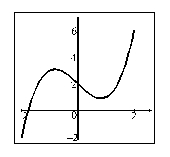
(Short Answer)
4.7/5  (32)
(32)
The graph of a function is given. Determine the average rate of change of the function between the indicated points on the graph.
(2,8) 
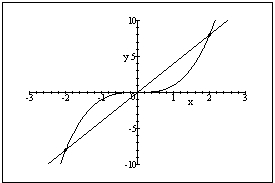
(Essay)
5.0/5  (41)
(41)
Let . Graph the family of functions with , , , , and in the viewing rectangle by . How does the value of affect the graph?
(Essay)
4.7/5  (35)
(35)
A function is given.
(a) Find all the local maximum and minimum values of the function and the value of x at which each occurs.
(b) Find the intervals on which the function is increasing and on which the function is decreasing. State all answers correct to two decimal places.
(Essay)
4.9/5  (35)
(35)
Determine whether or not the function given by the graph is one-to-one. 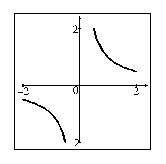
(Short Answer)
4.9/5  (36)
(36)
The graph of a function h is given.
(a) Find
(b) Find the domain and range of h.
(c) Find the values of x for which
(d) Find the values of x for which
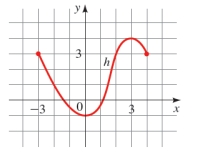
(Essay)
4.8/5  (35)
(35)
Determine if the equation defines as a function of . Explain your answer.
(Essay)
4.9/5  (41)
(41)
Use a graphing device to draw the graph of the function . State approximately the intervals on which the function is increasing and on which the function is decreasing.
(Essay)
4.8/5  (44)
(44)
A function is given.
(a) Find all the local maximum and minimum values of the function and the value of x at which each occurs.
(b) Find the intervals on which the function is increasing and on which the function is decreasing. State all answers correct to two decimal places.
(Essay)
4.9/5  (43)
(43)
Showing 61 - 80 of 98
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)