Exam 8: First-Order Differential Equations
Exam 1: Preliminaries143 Questions
Exam 2: Limits and Continuity125 Questions
Exam 3: Differentiation150 Questions
Exam 4: Applications of the Derivative143 Questions
Exam 5: Integration154 Questions
Exam 6: Applications of the Definite Integral113 Questions
Exam 7: Integration Techniques95 Questions
Exam 8: First-Order Differential Equations72 Questions
Exam 9: Infinite Series111 Questions
Exam 10: Parametric Equations and Polar Coordinates129 Questions
Exam 11: Vectors and the Geometry of Space107 Questions
Exam 12: Vector-Valued Functions103 Questions
Exam 13: Functions of Several Variables and Partial Differentiation112 Questions
Exam 14: Multiple Integrals92 Questions
Exam 15: Vector Calculus67 Questions
Exam 16: Second Order Differential Equations38 Questions
Select questions type
Match the appropriate slope field with the differential equation 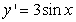 .
.
(Multiple Choice)
4.9/5  (40)
(40)
Use the following direction field to identify the stability of the equilibrium point (0.57, 0.14). 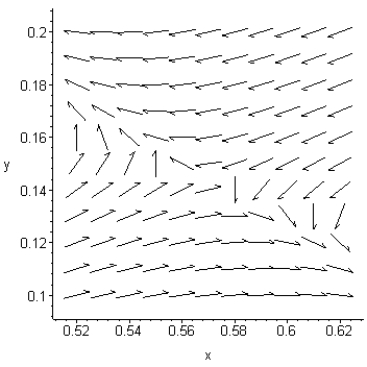
(Multiple Choice)
4.7/5  (42)
(42)
The conversion of sucrose (table sugar) to glucose and fructose is first order in the concentration of sucrose, which means that the rate of reaction is proportional to the concentration of the sucrose. The rate of disappearance of sucrose can be expressed as 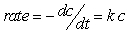 , where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If the rate constant is 0.20 hour-1, how long will it take for the sucrose concentration to diminish to 1/20 of its initial concentration?
, where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If the rate constant is 0.20 hour-1, how long will it take for the sucrose concentration to diminish to 1/20 of its initial concentration?
(Multiple Choice)
4.8/5  (46)
(46)
Find and interpret all equilibrium points for the competing species model. 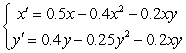
(Essay)
4.8/5  (44)
(44)
The population of New Zealand grew exponentially through the 20th century at a rate of 1.6% year-1. If the population in 2000 was 3.9 million, when was the population 1.0 million?
(Multiple Choice)
4.8/5  (34)
(34)
In 1965, Fairchild Semiconductor's R&D Director, Gordon Moore, noted that the maximum number of transistors that could be included cost effectively in one integrated circuit had been doubling yearly since 1959. While growth has not increased quite as quickly since 1965, it has still been exponential, and the continued exponential growth has become known as "Moore's Law". Considering that Intel's 8086 processor, introduced in 1978, had 29,000 transistors, and their Itanium processor, introduced in 2002, had 220,000,000 transistors, on average how long has it taken for processors to double the number of transistors they use.
(Multiple Choice)
4.8/5  (40)
(40)
Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k1, and C can decompose to make A and B in a first order reaction with rate constant of k-1. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A0, B0, and C0, the change in C can be represented with the differential equation ![Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k<sub>1</sub>, and C can decompose to make A and B in a first order reaction with rate constant of k<sub>-1</sub>. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A<sub>0</sub>, B<sub>0</sub>, and C<sub>0</sub>, the change in C can be represented with the differential equation . If A<sub>0</sub> = 0 , B<sub>0</sub> = 0, C<sub>0</sub> = 4, k<sub>1</sub> = 0.02 s <sup>-1</sup>, and k<sub>-1</sub> = 0.04 s<sup> -1</sup>, how much C is present after 15 seconds? [Note: c cannot be larger than C<sub>0</sub> plus the smaller of A<sub>0</sub> or B<sub>0</sub>. Nor can it be smaller than 0.]](https://storage.examlex.com/TB2342/11eaa948_cce7_4748_84bc_99030ba301d4_TB2342_00.jpg) . If A0 = 0 , B0 = 0, C0 = 4, k1 = 0.02 s -1, and k-1 = 0.04 s -1, how much C is present after 15 seconds? [Note: c cannot be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
. If A0 = 0 , B0 = 0, C0 = 4, k1 = 0.02 s -1, and k-1 = 0.04 s -1, how much C is present after 15 seconds? [Note: c cannot be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
(Multiple Choice)
5.0/5  (27)
(27)
Find the solution to the following separable differential equation. 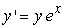
(Multiple Choice)
4.9/5  (46)
(46)
Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.] ![Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.]](https://storage.examlex.com/TB2342/11eaa948_cce7_e393_84bc_f1ca76292265_TB2342_11.jpg)
(Essay)
4.9/5  (36)
(36)
Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.] ![Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.]](https://storage.examlex.com/TB2342/11eaa948_cce7_e395_84bc_855d6d681471_TB2342_11.jpg)
(Essay)
5.0/5  (40)
(40)
Showing 61 - 72 of 72
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)