Exam 14: Multiple Integrals
Exam 1: Preliminaries143 Questions
Exam 2: Limits and Continuity125 Questions
Exam 3: Differentiation150 Questions
Exam 4: Applications of the Derivative143 Questions
Exam 5: Integration154 Questions
Exam 6: Applications of the Definite Integral113 Questions
Exam 7: Integration Techniques95 Questions
Exam 8: First-Order Differential Equations72 Questions
Exam 9: Infinite Series111 Questions
Exam 10: Parametric Equations and Polar Coordinates129 Questions
Exam 11: Vectors and the Geometry of Space107 Questions
Exam 12: Vector-Valued Functions103 Questions
Exam 13: Functions of Several Variables and Partial Differentiation112 Questions
Exam 14: Multiple Integrals92 Questions
Exam 15: Vector Calculus67 Questions
Exam 16: Second Order Differential Equations38 Questions
Select questions type
A function 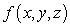 is a pdf on the three-dimensional region Q if
is a pdf on the three-dimensional region Q if 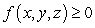 for all
for all 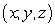 in Q and
in Q and 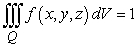 . Find k such that
. Find k such that 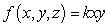 is a pdf on the region bounded by z = 0, z = 3, x = 0, x = 2, y - z = 0 , and y - z = 3.
is a pdf on the region bounded by z = 0, z = 3, x = 0, x = 2, y - z = 0 , and y - z = 3.
(Multiple Choice)
4.8/5  (37)
(37)
Find the volume of the given solid Q. Q is bounded by x - 4z = -1, x - 4z = 2, -2y + 3z = 3, -2y + 3z = 5, -4y + z = 1, and -4y + z = 2.
(Multiple Choice)
5.0/5  (29)
(29)
A skydiving club is having a competition to see who can land the closest to a target point. Jeff is a highly experienced skydiver, and the probability that he will land inside a region R is given by 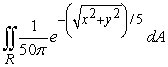 , where the coordinate system is centered on the target point. Compute the probability that Jeff lands within 11 feet of the target point.
, where the coordinate system is centered on the target point. Compute the probability that Jeff lands within 11 feet of the target point. 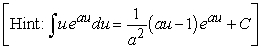
(Multiple Choice)
4.8/5  (35)
(35)
Evaluate the iterated integral by first changing the order of integration. 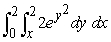
(Multiple Choice)
4.8/5  (23)
(23)
Find an integral equal to the volume of the solid bounded by the given surfaces and evaluate the integral. 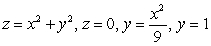
(Essay)
4.9/5  (34)
(34)
Find a transformation from a rectangular region S in the uv-plane to the region R which is bounded by 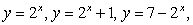 and
and 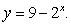
(Multiple Choice)
4.9/5  (35)
(35)
Use an appropriate coordinate system to compute the volume of the solid below 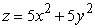 , above
, above 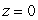 and inside
and inside 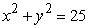 .
.
(Multiple Choice)
4.9/5  (34)
(34)
Set up and evaluate the integral 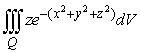 where Q is the region above the xy-plane bounded by the hemisphere centered at (0,0,0) and with a radius of 5.
where Q is the region above the xy-plane bounded by the hemisphere centered at (0,0,0) and with a radius of 5.
(Multiple Choice)
4.8/5  (30)
(30)
Evaluate the iterated integral by first changing the order of integration. 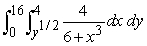
(Multiple Choice)
4.8/5  (26)
(26)
Evaluate the integral 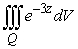 , where Q is the region with z > 0 bounded by
, where Q is the region with z > 0 bounded by 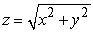 and
and 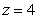 .
.
(Multiple Choice)
4.8/5  (41)
(41)
Find the surface area of the portion of 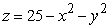 above the xy plane.
above the xy plane.
(Multiple Choice)
4.9/5  (34)
(34)
Find the mass of the solid with density 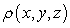 and the given shape.
and the given shape. 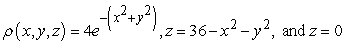 ,
,
(Multiple Choice)
4.8/5  (37)
(37)
Showing 41 - 60 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)