Exam 39: More About Matter Waves
Exam 1: Measurement37 Questions
Exam 2: Motion Along a Straight Line90 Questions
Exam 3: Vector37 Questions
Exam 4: Motion in Two and Three Dimensions56 Questions
Exam 5: Force and Motion I73 Questions
Exam 6: Force and Motion II74 Questions
Exam 7: Kinetic Energy and Work73 Questions
Exam 8: Potential Energy and Conservation of Energy63 Questions
Exam 9: Center of Mass and Linear Momentum99 Questions
Exam 10: Rotation102 Questions
Exam 11: Rolling, Torque, and Angular Momentum66 Questions
Exam 12: Equilibrium and Elasticity57 Questions
Exam 13: Gravitation55 Questions
Exam 14: Fluids88 Questions
Exam 15: Oscillations75 Questions
Exam 16: Waves I82 Questions
Exam 17: Waves II71 Questions
Exam 18: Temperature, Heat, and the First Law of Thermodynamics96 Questions
Exam 19: The Kinetic Theory of Gases113 Questions
Exam 20: Entropy and the Second Law of Thermodynamics61 Questions
Exam 21: Electric Charge52 Questions
Exam 22: Electric Fields55 Questions
Exam 23: Gauss Law38 Questions
Exam 24: Electric Potential52 Questions
Exam 25: Capacitance61 Questions
Exam 26: Current and Resistance55 Questions
Exam 27: Circuits73 Questions
Exam 28: Magnetic Fields55 Questions
Exam 29: Magnetic Fields Due to Currents49 Questions
Exam 30: Induction and Inductance90 Questions
Exam 31: Electromagnetic Oscillations and Alternating Current88 Questions
Exam 32: Maxwells Equations; Magnetism of Matter81 Questions
Exam 33: Electromagnetic Waves83 Questions
Exam 34: Images79 Questions
Exam 35: Interference46 Questions
Exam 36: Diffraction77 Questions
Exam 37: Relativity68 Questions
Exam 38: Photons and Matter Waves57 Questions
Exam 39: More About Matter Waves41 Questions
Exam 40: All About Atoms79 Questions
Exam 41: Conduction of Electricity in Solids51 Questions
Exam 42: Nuclear Physics68 Questions
Exam 43: Energy From the Nucleus50 Questions
Exam 44: Quarks, Leptons, and the Big Bang55 Questions
Select questions type
The figure shows the energy levels for an electron in a finite potential energy well. If an electron in the n = 2 state absorbs a photon of wavelength 2.0 nm, what happens to the electron? 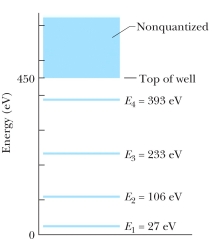
(Multiple Choice)
4.9/5  (29)
(29)
The ground state energy of an electron in a one-dimensional trap with zero potential energy in the interior and infinite potential energy at the walls is 2.0 eV. If the width of the well is doubled, the ground state energy will be:
(Multiple Choice)
4.9/5  (33)
(33)
Take the potential energy of a hydrogen atom to be zero for infinite separation of the electron and proton. Then, according to the quantum theory the energy En of a state with principal quantum number n is proportional to:
(Multiple Choice)
4.8/5  (33)
(33)
Take the potential energy of a hydrogen atom to be zero for infinite separation of the electron and proton. Then the ground state energy of a hydrogen atom is -13.6 eV. The minus sign indicates:
(Multiple Choice)
4.9/5  (37)
(37)
A particle is confined to a one-dimensional trap by infinite potential energy walls. Of the following states, designed by the quantum number n, for which one is the probability density greatest near the center of the well?
(Multiple Choice)
4.9/5  (34)
(34)
Take the potential energy of a hydrogen atom to be zero for infinite separation of the electron and proton. Then the ground state energy of a hydrogen atom is -13.6 eV. When the electron is in the first excited state its excitation energy (the difference between the energy of the state and that of the ground state) is:
(Multiple Choice)
4.8/5  (30)
(30)
An electron is in a one-dimensional trap with zero potential energy in the interior and infinite potential energy at the walls. A graph of its wave function (x) versus x is shown. The value of quantum number n is: 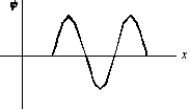
(Multiple Choice)
4.9/5  (38)
(38)
The wave function for an electron in a state with zero angular momentum:
(Multiple Choice)
4.9/5  (40)
(40)
A particle is trapped in an infinite potential energy well. It is in the state with quantum number n = 14. How many nodes does the probability density have (counting the nodes at the ends of the well)?
(Multiple Choice)
4.9/5  (29)
(29)
Take the potential energy of a hydrogen atom to be zero for infinite separation of the electron and proton. Then the ground state energy of a hydrogen atom is -13.6 eV. The energy of the first excited state is:
(Multiple Choice)
4.9/5  (35)
(35)
A particle is confined by finite potential energy walls to a one-dimensional trap from x = 0 to x = L. Its wave function in the region x > L has the form:
(Multiple Choice)
4.8/5  (36)
(36)
The figure shows the energy levels for an electron in a finite potential energy well. If the electron makes a transition from the n = 3 state to the ground state, what is the wavelength of the emitted photon? 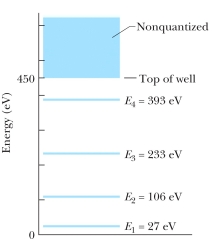
(Multiple Choice)
5.0/5  (33)
(33)
The following image is a dot plot of the ground state of the hydrogen atom. The dots represent: 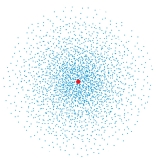
(Multiple Choice)
4.7/5  (38)
(38)
A particle is trapped in a one-dimensional well with infinite potential energy at the walls. Three possible pairs of energy levels are 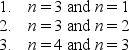 Order these pairs according to the difference in energy, least to greatest.
Order these pairs according to the difference in energy, least to greatest.
(Multiple Choice)
4.9/5  (40)
(40)
If the wave function is spherically symmetric then the radial probability density is given by:
(Multiple Choice)
4.8/5  (36)
(36)
Consider the following: 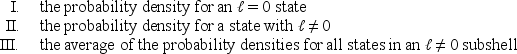 Of these which are spherically symmetric?
Of these which are spherically symmetric?
(Multiple Choice)
4.7/5  (39)
(39)
If a wave function for a particle moving along the x axis is "normalized" then:
(Multiple Choice)
4.8/5  (30)
(30)
An electron in an atom initially has an energy 5.5 eV above the ground state energy. It drops to a state with energy 3.2 eV above the ground state energy and emits a photon in the process. The wave associated with the photon has a wavelength of:
(Multiple Choice)
4.8/5  (43)
(43)
The radial probability density for the electron in the ground state of a hydrogen atom has a peak at about:
(Multiple Choice)
4.9/5  (41)
(41)
Showing 21 - 40 of 41
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)