Exam 2: Linear Programming: Model Formulation and Graphical Solution

Multiple optimal solutions can occur when the objective function is ________ a constraint line.

When using the graphical method, only one of the four quadrants of an xy-axis needs to be drawn.

Graphical solutions to linear programming problems have an infinite number of possible objective function lines.

________ are at the endpoints of the constraint line segment that the objective function parallels.

A linear programming problem that results in a solution that is ________ usually indicates that the linear program has been incorrectly formulated.

In the graphical approach, simultaneous equations may be used to solve for the optimal solution point.

The following is a graph of a linear programming problem. The feasible solution space is shaded, and the optimal solution is at the point labeled Z*. 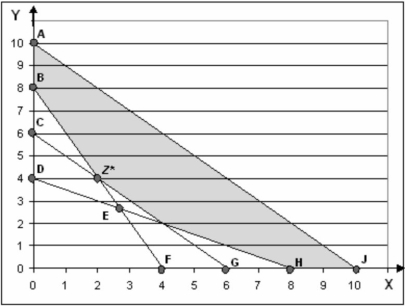-Which of the following points is not feasible?

A linear programming model consists of

In the formulation of a ≥ constraint,

________ is the difference between the left- and right-hand sides of a greater than or equal to constraint.

In a linear programming problem, the binding constraints for the optimal solution are: 5x1 + 3x2 ≤ 30 2x1 + 5x2 ≤ 20 Which of these objective functions will lead to the same optimal solution?

Consider the following linear programming problem: MIN Z =   & 2x1 + 3x2 Subject to:    x1 + 2x2 ? 20     5x1 + x2 ? 40     4x1 +6x2 ? 60     x1 , x2 ? 0 What is the optimal solution?

The poultry farmer decided to make his own chicken scratch by combining alfalfa and corn in rail car quantities. A rail car of corn costs $400 and a rail car of alfalfa costs $200. The farmer's chickens have a minimum daily requirement of vitamin K (500 milligrams) and iron (400 milligrams), but it doesn't matter whether those elements come from corn, alfalfa, or some other grain. A unit of corn contains 150 milligrams of vitamin K and 75 milligrams of iron. A unit of alfalfa contains 250 milligrams of vitamin K and 50 milligrams of iron. Formulate the linear programming model for this situation.

A graphical representation of a linear program is shown below. The shaded area represents the feasible region, and the dashed line in the middle is the slope of the objective function. 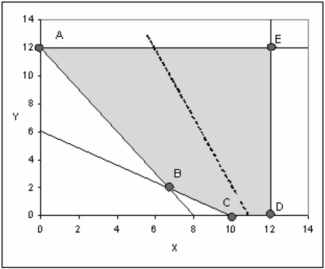What would the be the new slope of the objective function if multiple optimal solutions occurred along line segment AB?

The ________ property of linear programming models indicates that the values of all the model parameters are known and are assumed to be constant.

Which of the following could not be a linear programming problem constraint?

The production manager for the Coory soft drink company is considering the production of two kinds of soft drinks: regular and diet. Two of her limited resources are production time (8 hours = 480 minutes per day) and syrup (1 of the ingredients), limited to 675 gallons per day. To produce a regular case requires 2 minutes and 5 gallons of syrup, while a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case. For the production combination of 135 cases of regular and 0 cases of diet soft drink, which resources will not be completely used?

________ is used to analyze changes in model parameters.

The objective function is a linear relationship reflecting the objective of an operation.

Which of the following special cases does not require reformulation of the problem in order to obtain a solution?