Exam 2: Linear Programming: Model Formulation and Graphical Solution

A company producing a standard line and a deluxe line of dishwashers has the following time requirements (in minutes) in departments where either model can be processed. Standard Deluxe Stamping 3 6 Motor installation 10 10 Wiring 10 15 The standard models contribute $20 each and the deluxe $30 each to profits. Because the company produces other items that share resources used to make the dishwashers, the stamping machine is available only 30 minutes per hour, on average. The motor installation production line has 60 minutes available each hour. There are two lines for wiring, so the time availability is 90 minutes per hour. Let x = number of standard dishwashers produced per hour y = number of deluxe dishwashers produced per hour Write the formulation for this linear program.

The production manager for the Coory soft drink company is considering the production of two kinds of soft drinks: regular (R) and diet(D). Two of the limited resources are production time (8 hours = 480 minutes per day) and syrup (1 of the ingredients), limited to 675 gallons per day. To produce a regular case requires 2 minutes and 5 gallons of syrup, while a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case. What is the time constraint?

Objective functions in linear programs always minimize costs.

Cully Furniture buys two products for resale: big shelves (B) and medium shelves (M). Each big shelf costs $500 and requires 100 cubic feet of storage space, and each medium shelf costs $300 and requires 90 cubic feet of storage space. The company has $75,000 to invest in shelves this week, and the warehouse has 18,000 cubic feet available for storage. Profit for each big shelf is $300 and for each medium shelf is $150. In order to maximize profit, how many big shelves (B) and how many medium shelves (M) should be purchased?

The ________ solution area is an area bounded by the constraint equations.

Which of these statements is best?

The following is a graph of a linear programming problem. The feasible solution space is shaded, and the optimal solution is at the point labeled Z*. 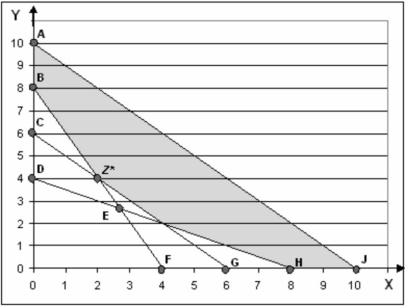-This linear programming problem is a(n)

Consider the following linear programming problem: MIN Z =    3x1 + 2x2 Subject to:    2x1 + 3x2 ? 12     5x1 + 8x2 ? 37     x1, x2 ? 0 At the optimal solution point, the objective function value is 18. If the constraints are changed from greater than to less than constraints and the objective function is changed from minimize to maximize, what happens to the optimal solution? Demonstrate whether it falls at the same optimal point.

Consider the following linear programming problem: MIN Z =    10x1 + 20x2 Subject to:    x1 + x2 ? 12     2x1 + 5x2 ? 40     x2 ? 13     x1, x2 ? 0 At the optimal solution, what is the value of surplus associated with constraint 1 and constraint 3, respectively?

A slack variable

When a maximization problem is ________, the objective function can increase indefinitely without reaching a maximum value.

If the feasible region for a linear programming problem is unbounded, then the solution to the corresponding linear programming problem is ________ unbounded.

The optimal solution of a minimization problem is at the extreme point ________ the origin.

The ________ property of linear programming models indicates that the rate of change or slope of the objective function or a constraint is constant.

The production manager for the Coory soft drink company is considering the production of two kinds of soft drinks: regular and diet. Two of her limited resources are production time (8 hours = 480 minutes per day) and syrup (1 of the ingredients), limited to 675 gallons per day. To produce a regular case requires 2 minutes and 5 gallons of syrup, while a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case. Which of the following is not a feasible production combination?

A feasible solution violates at least one of the constraints.

The constraint 2X +XY violates the ________ property of linear programming.

If the objective function is parallel to a constraint, the linear program could have ________.

Which of the following could be a linear programming objective function?

If at least one constraint in a linear programming model is violated, the solution is said to be ________.