Graph the Hyperbola $x ^ { 2 } - 25 y ^ { 2 } = 25$

Multiple Choice

Graph the hyperbola. Specify the following: vertices, foci, lengths of transverse and conjugate axes, eccentricity, and equations of the asymptotes. $x ^ { 2 } - 25 y ^ { 2 } = 25$

A) 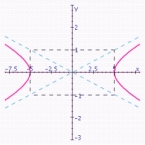vertices: $( \pm 5,0 )$ ;
Foci: $( \pm \sqrt { 26 } , 0 )$ ;
Length of transverse axis: 10;
Length of conjugate axis: 2;
Eccentricity: $\frac { \sqrt { 26 } } { 5 }$
Asymptotes: $y = \pm \frac { 1 } { 5 } x$ .
B) 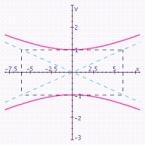vertices: $( 0 , \pm 6 )$ ;
Foci: $( 0 , \pm \sqrt { 37 } )$ ;
Length of transverse axis: 2;
Length of conjugate axis: 12;
Eccentricity: $\sqrt { 37 }$ ;
Asymptotes: $y = \pm \frac { 1 } { 6 } x$ .
C) 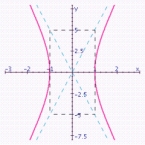vertices: $( \pm 1,0 )$ ;
Foci: $( \pm \sqrt { 26 } , 0 )$ ;
Length of transverse axis: 2;
Length of conjugate axis: 10;
Eccentricity: $\sqrt { 26 }$ ;
Asymptotes: $y = \pm 5 x$ .
D) 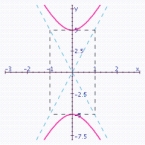vertices: $( 0 , \pm 5 )$ ;
Foci: $( 0 , \pm \sqrt { 26 } )$ ;
Length of transverse axis: 10;
Length of conjugate axis: 2;
Eccentricity: $\frac { \sqrt { 26 } } { 5 }$
Asymptotes: $y = \pm 5 x$ .
E) 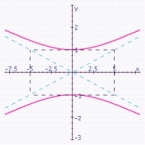vertices: $( 0 , \pm 1 )$ ;
Foci: $( 0 , \pm \sqrt { 26 } )$ ;
Length of transverse axis: 2;
Length of conjugate axis: 10;
Eccentricity: $\sqrt { 26 }$ ;
Asymptotes: $y = \pm \frac { 1 } { 5 } x$ .