Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming
Exam 1: Introduction to Quantitative Analysis63 Questions
Exam 2: Probability Concepts and Applications145 Questions
Exam 3: Decision Analysis119 Questions
Exam 4: Regression Models120 Questions
Exam 5: Forecasting101 Questions
Exam 6: Inventory Control Models113 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods100 Questions
Exam 8: Linear Programming Applications96 Questions
Exam 9: Transportation and Assignment Models80 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming88 Questions
Exam 11: Network Models86 Questions
Exam 12: Project Management123 Questions
Exam 13: Waiting Lines and Queuing Theory Models133 Questions
Exam 14: Simulation Modeling68 Questions
Exam 15: Markov Analysis78 Questions
Exam 16: Statistical Quality Control87 Questions
Select questions type
Consider the following 0-1 integer programming problem: 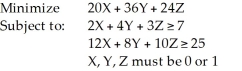 If we wish to add the constraint that no more than two of these variables must be positive, how would this be written?
If we wish to add the constraint that no more than two of these variables must be positive, how would this be written?
(Multiple Choice)
4.8/5  (41)
(41)
A goal programming problem had two goals (with no priorities assigned). Goal number 1 was to achieve a cost of $3,600 and goal number 2 was to complete the task in 400 hours or fewer. The optimal solution to this problem resulted in a cost of $3,600 and a completion time of 420 hours. What was the value for the objective function for this goal programming problem?
(Multiple Choice)
4.8/5  (30)
(30)
0-1 integer programming might be applicable to selecting the best gymnastics team to represent a country from among all identified teams.
(True/False)
4.9/5  (31)
(31)
Table 10-1
A company has decided to use 0-1 integer programming to help make some investment decisions. There are three possible investment alternatives from which to choose, but if it is decided that a particular alternative is to be selected, the entire cost of that alternative will be incurred (i.e., it is impossible to build one-half of a factory). The integer programming model is as follows:  The optimal solution is X1 = 0, X2 = 1, X3 = 1
-In Table 10-1, which presents an integer programming problem, using the optimal solution means only two of the alternatives would be selected. How much slack is there in the third constraint?
The optimal solution is X1 = 0, X2 = 1, X3 = 1
-In Table 10-1, which presents an integer programming problem, using the optimal solution means only two of the alternatives would be selected. How much slack is there in the third constraint?
(Multiple Choice)
4.7/5  (39)
(39)
An integer programming (minimization) problem was first solved as a linear programming problem, and the objective function value (cost) was $253.67. The two decision variables (X, Y) in the problem had values of X = 12.45 and Y = 32.75. If there is a single optimal solution, which of the following must be true for the optimal integer solution to this problem?
(Multiple Choice)
4.7/5  (40)
(40)
Unfortunately, multiple goals in goal programming are not able to be prioritized and solved.
(True/False)
5.0/5  (38)
(38)
Table 10-2  -According to Table 10-2, which presents a solution for an integer programming problem, at the optimal solution, how much slack exists in the third constraint?
-According to Table 10-2, which presents a solution for an integer programming problem, at the optimal solution, how much slack exists in the third constraint?
(Multiple Choice)
4.9/5  (37)
(37)
Assignment problems solved previously by linear programming techniques are also examples of
(Multiple Choice)
4.9/5  (43)
(43)
Table 10-4
A company has decided to use 0−1 integer programming to help make some investment decisions. There are three possible investment alternatives from which to choose, but if it is decided that a particular alternative is to be selected, the entire cost of that alternative will be incurred (i.e., it is impossible to build one-half of a factory). The integer programming model is as follows:  -Table 10-4 presents an integer programming problem. If the optimal solution is used, then only two of the alternatives would be selected. How much slack would there be in the third constraint?
-Table 10-4 presents an integer programming problem. If the optimal solution is used, then only two of the alternatives would be selected. How much slack would there be in the third constraint?
(Multiple Choice)
4.9/5  (33)
(33)
The concept of a local optimum is affiliated with which of the following?
(Multiple Choice)
5.0/5  (40)
(40)
A 0-1 programming representation could be used to assign sections of a course to specific classrooms.
(True/False)
4.9/5  (35)
(35)
If conditions require that all decision variables must have an integer solution, then the class of problem described is an integer programming problem.
(True/False)
4.9/5  (34)
(34)
The overall best solution in a nonlinear program is a ________.
(Multiple Choice)
4.7/5  (38)
(38)
Table 10-4
A company has decided to use 0−1 integer programming to help make some investment decisions. There are three possible investment alternatives from which to choose, but if it is decided that a particular alternative is to be selected, the entire cost of that alternative will be incurred (i.e., it is impossible to build one-half of a factory). The integer programming model is as follows:  -Table 10-4 presents an integer programming problem. What is the meaning of Constraint 1?
-Table 10-4 presents an integer programming problem. What is the meaning of Constraint 1?
(Multiple Choice)
4.7/5  (31)
(31)
A goal programming problem had two goals (with no priorities assigned). Goal number 1 was to achieve a cost of $3,600 and goal number 2 was to have no wasted material. The optimal solution to this problem resulted in a cost of $3,900 and no wasted material. What was the value for the objective function for this goal programming problem?
(Multiple Choice)
4.7/5  (43)
(43)
Showing 41 - 60 of 88
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)