Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming

When solving very large integer programming problems, we sometimes have to settle for a "good," not necessarily optimal, answer.

We do not have a general method for solving all types of ________ problems.

Smalltime Investments Inc. is going to purchase new computers. There are ten employees, and the company would like one for each employee. The cost of the basic personal computer with monitor and disk drive is $2,000, while the deluxe version with VGA and advanced processor is $3,500. Due to internal politics, the number of deluxe computers should be less than half the number of regular computers, but at least three deluxe computers must be purchased. The budget is $27,000, although additional money could be used if it were deemed necessary. All of these are goals that the company has identified. Formulate this as a goal programming problem.

Table 10-1 A company has decided to use 0-1 integer programming to help make some investment decisions. There are three possible investment alternatives from which to choose, but if it is decided that a particular alternative is to be selected, the entire cost of that alternative will be incurred (i.e., it is impossible to build one-half of a factory). The integer programming model is as follows: The optimal solution is X₁ = 0, X₂ = 1, X₃ = 1 -According to Table 10-1, which presents an integer programming problem, if the optimal solution is used, how much of the budget would be spent?

Table 10-6 -Table 10-6 represents a solution for an integer programming problem. If this problem had been solved as a simple linear programming problem, what would you expect the value of the objective function to be?

Unfortunately, goal programming, while able to handle multiple objectives, is unable to prioritize these objectives.

An integer programming (maximization) problem was first solved as a linear programming problem, and the objective function value (profit) was $253.67. The two decision variables (X, Y) in the problem had values of X = 12.45 and Y = 32.75. If there is a single optimal solution, which of the following must be true for the optimal integer solution to this problem?

In a goal programming problem with two goals at the same priority level, all the deviational variables are equal to zero in the optimal solution. This means

A bakery produces muffins and doughnuts. Let x₁ be the number of doughnuts produced and x₂ be the number of muffins produced. The profit function for the bakery is expressed by the following equation: profit = 4x₁ + 2x₂ + 0.3x₁² + 0.4x₂². The bakery has the capacity to produce 800 units of muffins and doughnuts combined and it takes 30 minutes to produce 100 muffins and 20 minutes to produce 100 doughnuts. There is a total of 4 hours available for baking time. There must be at least 200 units of muffins and at least 200 units of doughnuts produced. Formulate a nonlinear program representing the profit maximization problem for the bakery.

In goal programming, if all the goals are achieved, then the value of the objective function will always be zero.

The transportation problem is a good example of a pure integer programming problem.

A quadratic programming problem involves which of the following conditions?

A goal programming problem had two goals (with no priorities assigned). Goal number 1 was to achieve a profit of $2,400 and goal number 2 was to have no idle time for workers in the factory. The optimal solution to this problem resulted in a profit of $2,300 and no idle time. What was the value for the objective function for this goal programming problem?

In goal programming, the deviational variables have the same objective function coefficients as the surplus and slack variables in a normal linear program.

Smalltime Investments Inc. is going to purchase new computers for most of the employees. There are ten employees, and at least eight computers must be purchased. The cost of the basic personal computer with monitor and disk drive is $2,000, while the deluxe version with VGA and advanced processor is $3,500. Due to internal politics, the number of deluxe computers must be no more than half the number of regular computers, but at least three deluxe computers must be purchased. The budget is $27,000. Formulate this as an integer programming problem to maximize the number of computers purchased.

Which of the following statements is false concerning goal programming?

Requiring an integer solution to a linear programming problem decreases the size of the feasible region.

A capital budgeting problem involving the selection of possible projects under budget constraints is solved by which of the following?

As part of a larger problem, you are trying to determine whether or not to open a plant with a capacity of 10,000 units (using binary variable Y). You also define X as the number of units (if any) produced at that plant. How will you ensure that Y will equal 1 if the plant is open?

Table 10-5 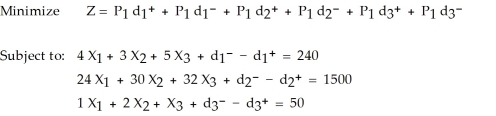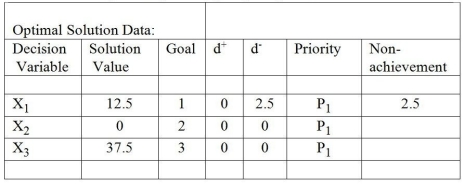-Table 10-5 represents a solution to a goal programming problem. There are three goals (each represented by a constraint). Which goals are only partly achieved?