Question 1

Goal programming and linear programming differ in that

Accepted Answer

A)  in LP, the objective function is maximized or minimized, while in goal programming, the deviation between goals and possible achievement is minimized. 
B)  slack variables are used in LP, while deviational variables are used in goal programming. 
C)  deviational variables have positive objective function coefficients in goal programming, but slack variables have 0 coefficients in LP. 
D)  All of the above 
E)  None of the above 
A)  in LP, the objective function is maximized or minimized, while in goal programming, the deviation between goals and possible achievement is minimized. 
B)  slack variables are used in LP, while deviational variables are used in goal programming. 
C)  deviational variables have positive objective function coefficients in goal programming, but slack variables have 0 coefficients in LP. 
D)  All of the above 
E)  None of the above

Question 2

Table 10-5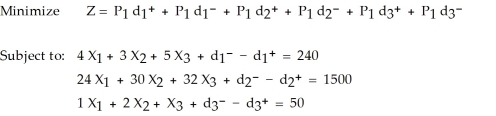    
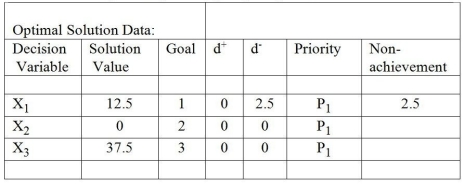-Table 10-5 represents a solution to a goal programming problem. There are three goals (each represented by a constraint). Which of the goals is assigned the highest priority?

Accepted Answer

A)  goal 1 
B)  goal 2 
C)  goal 3 
D)  goals 2 and 3 
E)  All goals have the same priority. 
A)  goal 1 
B)  goal 2 
C)  goal 3 
D)  goals 2 and 3 
E)  All goals have the same priority.

Question 3

An integer programming (maximization) problem was first solved as a linear programming problem, and the objective function value (profit) was $253.67. The two decision variables (X, Y) in the problem had values of X = 12.45 and Y = 32.75. Which of the following must be true for the optimal integer solution to this problem?

Accepted Answer

A)  X = 12 Y = 32 
B)  X = 12 Y = 33 
C)  X = 12 
D)  Y = 32 
E)  None of the above 
A)  X = 12 Y = 32 
B)  X = 12 Y = 33 
C)  X = 12 
D)  Y = 32 
E)  None of the above

Question 4

The Elastic Firm has two products coming on the market: Zigs and Zags. To make a Zig, the firm needs 10 units of product A and 15 units of product B. To make a Zag, they need 20 units of product A and 15 units of product B. There are only 2,000 units of product A and 3,200 units of product B available to the firm. The profit on a Zig is $4 and on a Zag it is $6. Management objectives in order of their priority are:
(1) Produce exactly 50 Zigs.
(2) Achieve a target profit of at least $750.
(3) Use all of the product B available.
Formulate this as a goal programming problem.

Accepted Answer

Let X₁ = number of Zigs, X₂ = number of Za

Question 5

A goal programming problem had two goals (with no priorities assigned). Goal number 1 was to achieve a profit of $3,600 and goal number 2 was to have no wasted material. The optimal solution to this problem resulted in a profit of $3,300 and no wasted material. What was the value for the objective function for this goal programming problem?

Accepted Answer

A)  300 
B)  -300 
C)  3300 
D)  0 
E)  None of the above 
A)  300 
B)  -300 
C)  3300 
D)  0 
E)  None of the above

Question 6

The Elastic Firm has two products coming on the market, Zigs and Zags. To make a Zig, the firm needs 10 units of product A and 15 units of product B. To make a Zag, they need 20 units of product A and 15 units of product B. There are only 2,000 units of product A and 3,000 units of product B available to the firm. The profit on a Zig is $4 and on a Zag it is $6. Management objectives in order of their priority are:
(1) Produce at least 40 Zags.
(2) Achieve a target profit of at least $750.
(3) Use all of the product A available.
(4) Use all of the product B available.
(5) Avoid the requirement for more product A.
Formulate this as a goal programming problem.

Accepted Answer

Let X₁ = number of Zigs, X₂ = number of Za

Question 7

Define deviational variables.

Accepted Answer

In goal programming, they cons

Question 8

The following objective function is nonlinear: Max 5X - 8YZ.

Accepted Answer

A) True 
 B)False

Question 9

Which of the following is not considered nonlinear programming?

Accepted Answer

A)  nonlinear objective and nonlinear constraints 
B)  linear objective with nonlinear constraints 
C)  nonlinear objective with linear constraints 
D)  binary decision variable with nonlinear constraints 
E)  integer decision variable with linear constraints 
A)  nonlinear objective and nonlinear constraints 
B)  linear objective with nonlinear constraints 
C)  nonlinear objective with linear constraints 
D)  binary decision variable with nonlinear constraints 
E)  integer decision variable with linear constraints

Question 10

Table 10-1
A company has decided to use 0-1 integer programming to help make some investment decisions. There are three possible investment alternatives from which to choose, but if it is decided that a particular alternative is to be selected, the entire cost of that alternative will be incurred (i.e., it is impossible to build one-half of a factory). The integer programming model is as follows:   The optimal solution is XS1U1B11S1U1B0 = 0, XS1U1B12S1U1B0 = 1, XS1U1B13S1U1B0 = 1
-According to Table 10-1, which presents an integer programming problem, the optimal solution is to select only two of the alternatives. Suppose you wished to add a constraint that stipulated that alternative 2 could only be selected if alternative 1 is also selected . How would this constraint be written?

Accepted Answer

A)  X1 = X2 
B)  X1 ≤ X2 
C)  X1 ≥ X2 
D)  X1 + X2 = 2 
E)  None of the above 
A)  X1 = X2 
B)  X1 ≤ X2 
C)  X1 ≥ X2 
D)  X1 + X2 = 2 
E)  None of the above

Question 11

If we wish to develop a stock portfolio wherein we maximize return and minimize risk, we would have to use

Accepted Answer

A)  pure-integer programming. 
B)  goal programming. 
C)  zero-one integer programming. 
D)  mixed-integer programming. 
E)  nonlinear programming. 
A)  pure-integer programming. 
B)  goal programming. 
C)  zero-one integer programming. 
D)  mixed-integer programming. 
E)  nonlinear programming.

Question 12

The three types of integer programs are: pure integer programming, impure integer programming, and 0-1 integer programming.

Accepted Answer

A) True 
 B)False

Question 13

Agile Bikes has manufacturing plants in Salt Lake City, Dallas, and Chicago. The Bikes are shipped to retail stores in Los Angeles, New York, Miami, and Seattle. Information on shipping costs, supply, and demand is given in the following table: 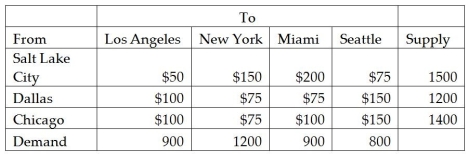  What type of mathematical programming is required to solve this problem?

Accepted Answer

zero-one i

Question 14

Table 10-1
A company has decided to use 0-1 integer programming to help make some investment decisions. There are three possible investment alternatives from which to choose, but if it is decided that a particular alternative is to be selected, the entire cost of that alternative will be incurred (i.e., it is impossible to build one-half of a factory). The integer programming model is as follows:   The optimal solution is XS1U1B11S1U1B0 = 0, XS1U1B12S1U1B0 = 1, XS1U1B13S1U1B0 = 1
-According to Table 10-1, which presents an integer programming problem, if the optimal solution is used, what would the value of the objective function be ________.

Accepted Answer

A)  21,000 
B)  12,000 
C)  16,000 
D)  2 
E)  None of the above 
A)  21,000 
B)  12,000 
C)  16,000 
D)  2 
E)  None of the above

Question 15

Quadratic programming contains squared terms in the constraints.

Accepted Answer

A) True 
 B)False

Question 16

Table 10-5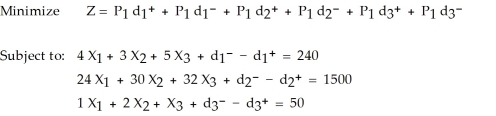    
-Table 10-5 represents a solution to a goal programming problem. There are three goals (each represented by a constraint). Goal number 3 represents a resource usage goal. How much of this resource would be used by this solution?

Accepted Answer

A)  50 units 
B)  70 units 
C)  2500 units 
D)  240 units 
E)  None of the above 
A)  50 units 
B)  70 units 
C)  2500 units 
D)  240 units 
E)  None of the above

Question 17

The concept of "satisficing" is affiliated with which of the following?

Accepted Answer

A)  mixed integer programming 
B)  integer programming 
C)  linear programming 
D)  nonlinear programming 
E)  goal programming 
A)  mixed integer programming 
B)  integer programming 
C)  linear programming 
D)  nonlinear programming 
E)  goal programming

Question 18

Define quadratic programming.

Accepted Answer

A quadratic programming proble

Question 19

Table 10-4
A company has decided to use 0−1 integer programming to help make some investment decisions. There are three possible investment alternatives from which to choose, but if it is decided that a particular alternative is to be selected, the entire cost of that alternative will be incurred (i.e., it is impossible to build one-half of a factory). The integer programming model is as follows:  
-Table 10-4 presents an integer programming problem. Suppose you wish to add a constraint that stipulates that both alternative 2 and alternative 3 must be selected, or neither can be selected. How would this constraint be written?

Accepted Answer

A)  X2 = X3 
B)  X2 ≤ X3 
C)  X2 ≥ X3 
D)  X2 + X3 = 1 
E)  None of the above 
A)  X2 = X3 
B)  X2 ≤ X3 
C)  X2 ≥ X3 
D)  X2 + X3 = 1 
E)  None of the above

Question 20

Another name for a 0-1 variable is a ________ variable.

Accepted Answer

A)  either-or 
B)  binary 
C)  yes-no 
D)  quadratic 
E)  on-off 
A)  either-or 
B)  binary 
C)  yes-no 
D)  quadratic 
E)  on-off

Goal programming and linear programming differ in that

Table 10-5 -Table 10-5 represents a solution to a goal programming problem. There are three goals (each represented by a constraint). Which of the goals is assigned the highest priority?

Define deviational variables.

The following objective function is nonlinear: Max 5X - 8YZ.

Which of the following is not considered nonlinear programming?

If we wish to develop a stock portfolio wherein we maximize return and minimize risk, we would have to use

The three types of integer programs are: pure integer programming, impure integer programming, and 0-1 integer programming.

Quadratic programming contains squared terms in the constraints.

Table 10-5 -Table 10-5 represents a solution to a goal programming problem. There are three goals (each represented by a constraint). Goal number 3 represents a resource usage goal. How much of this resource would be used by this solution?

The concept of "satisficing" is affiliated with which of the following?

Define quadratic programming.

Another name for a 0-1 variable is a ________ variable.

Introduction to Quantitative Analysis

Probability Concepts and Applications

Decision Analysis

Regression Models

Forecasting

Inventory Control Models

Linear Programming Models: Graphical and Computer Methods

Linear Programming Applications

Transportation and Assignment Models

Network Models

Project Management

Waiting Lines and Queuing Theory Models

Simulation Modeling

Markov Analysis

Statistical Quality Control

Filters

Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming

Goal programming and linear programming differ in that

Table 10-5 -Table 10-5 represents a solution to a goal programming problem. There are three goals (each represented by a constraint). Which of the goals is assigned the highest priority?

Define deviational variables.

The following objective function is nonlinear: Max 5X - 8YZ.

Which of the following is not considered nonlinear programming?

If we wish to develop a stock portfolio wherein we maximize return and minimize risk, we would have to use

The three types of integer programs are: pure integer programming, impure integer programming, and 0-1 integer programming.

Quadratic programming contains squared terms in the constraints.

Table 10-5 -Table 10-5 represents a solution to a goal programming problem. There are three goals (each represented by a constraint). Goal number 3 represents a resource usage goal. How much of this resource would be used by this solution?

The concept of "satisficing" is affiliated with which of the following?

Define quadratic programming.

Another name for a 0-1 variable is a ________ variable.

Introduction to Quantitative Analysis

Probability Concepts and Applications

Decision Analysis

Regression Models

Forecasting

Inventory Control Models

Linear Programming Models: Graphical and Computer Methods

Linear Programming Applications

Transportation and Assignment Models

Network Models

Project Management

Waiting Lines and Queuing Theory Models

Simulation Modeling

Markov Analysis

Statistical Quality Control

Filters