Question 1

Two methods of solving linear programming problems by hand include the corner-point method and the ________.

Accepted Answer

iso-profit (or iso-cost) line method

Question 2

In linear programming, statements such as "the blend must consist of at least 10% of ingredient A, at least 30% of ingredient B, and no more than 50% of ingredient C" can be made into valid constraints even though the percentages do not add up to 100%.

Accepted Answer

A) True 
 B)False  True

Question 3

In linear programming, a statement such as "maximize contribution" becomes a(n)

Accepted Answer

A)  constraint. 
B)  slack variable. 
C)  objective function. 
D)  violation of linearity. 
E)  decision variable. 
A)  constraint. 
B)  slack variable. 
C)  objective function. 
D)  violation of linearity. 
E)  decision variable. C

Question 4

In linear programming, if there are three constraints, each representing a resource that can be used up, the optimal solution must use up all of each of the three resources.

Accepted Answer

A) True 
 B)False

Question 5

What combination of x and y will yield the optimum for this problem? Maximize $3x + $15y, subject to (1) 2x + 4y < 12 and (2) 5x + 2y < 10 and (3) x, y ≥ 0.

Accepted Answer

A)  x = 2, y = 0 
B)  x = 0, y = 3 
C)  x = 0, y = 0 
D)  x = 1, y = 5 
E)  none of the above 
A)  x = 2, y = 0 
B)  x = 0, y = 3 
C)  x = 0, y = 0 
D)  x = 1, y = 5 
E)  none of the above

Question 6

The region that satisfies the constraint 4X + 15Z ≥ 1000 includes the origin of the graph.

Accepted Answer

A) True 
 B)False

Question 7

Lost Maples Winery makes three varieties of contemporary Constellation Country wines: Austin (a fine red), Ste. George (a table white), and Los Alamos (a hearty pink Zinfandel). The raw materials, labour, and contribution per case of each of these wines is summarized below.
 $$\begin{array} { | l | c | c | c | c | c | } 
\hline & \begin{array} { c } 
\text { Grapes } \
\text { Variety A } \
\text { bushels }
\end{array} & \begin{array} { c } 
\text { Grapes } \
\text { Variety B } \
\text { bushels }
\end{array} & \begin{array} { c } 
\text { Sugar } \
\text { KGS }
\end{array} & \begin{array} { c } 
\text { Labour (man- } \
\text { hours) }
\end{array} & \begin{array} { c } 
\text { Contrib. } \
\text { per case }
\end{array} \
\hline \text { Austin Formation } & 6 & 0 & 4 & 3 & \$ 27 \
\hline \text { Ste. Genevieve } & 0 & 4 & 1 & 1 & \$ 28 \
\hline \text { Los Alamos } & 2 & 1 & 2 & 2 & \$ 23 \
\hline
\end{array}$$ The winery has 3000 bushels of Variety A grapes, 2280 bushels of Variety B grapes, 1000 pounds of sugar, and 1400 man-hours of labour available during the next week. The firm operates to achieve maximum contribution. Refer to the POM for Windows panels showing the solution to this problem.
Answer the following questions.
a. For maximum contribution, how much of each wine should be produced?
b. How much contribution will be made by selling the output?
c. Is there any sugar left over? If so, how much?

Accepted Answer

(a) 0 cases of Austin Formatio

Question 8

The optimal solution of a linear programming problem that consists of two variables and six constraints will probably not satisfy all six constraints as equalities.

Accepted Answer

A) True 
 B)False

Question 9

A company has the following usage of inputs, constraints on inputs and profit margins to make their three products.
 $$\begin{array} { l l l l l } 
\text { Product } & \text { Wiring } & \text { Drilling } & \text { Assembly } & \text { Profit } \
\text { X202 } & 0.47 & 0.28 & 0.55 & 15 \
\text { Y303 } & 0.61 & 0.43 & 0.61 & 18 \
\text { Z404 } & 0.37 & 0.2 & 0.29 & 13.1
\end{array}$$ There are maximum amounts of the following: 1625 hours for wiring, 1750 hours for drilling and 1175 hours for Assembly. Make sure that the units produced are integers. Solve for the above problem. The company must make at least 825 X202, 475 Y303 and 625 Z404.
a) How many units of each product will be made?
b) What is the maximum profit?
c) Which input has the least amount of slack?

Accepted Answer

a)
 @#IMG-DLM& b)
 @#IMG-DLM& c) Assembly since it

Question 10

Two methods of conducting sensitivity analysis on solved linear programming problems are ________ and ________.

Accepted Answer

postoptima

Question 11

A linear programming problem has two constraints 2X + 4Y ≤ 100 and 1X + 8Y ≤ 100, plus nonnegativity constraints on X and Y. Which of the following statements about its feasible region is true?

Accepted Answer

A)  There are four corner points including (50, 0) and (0, 12.5). 
B)  The two corner points are (0, 0) and (50, 12.5). 
C)  The graphical origin (0, 0) is not in the feasible region. 
D)  The feasible region includes all points that satisfy one constraint, the other, or both. 
E)  The feasible region cannot be determined without knowing whether the problem is to be minimized or maximized. 
A)  There are four corner points including (50, 0) and (0, 12.5). 
B)  The two corner points are (0, 0) and (50, 12.5). 
C)  The graphical origin (0, 0) is not in the feasible region. 
D)  The feasible region includes all points that satisfy one constraint, the other, or both. 
E)  The feasible region cannot be determined without knowing whether the problem is to be minimized or maximized.

Question 12

A company has the following inputs and cost structure.
 $$\begin{array} { l l l l } 
\text { Product } & \mathrm { X } & \mathrm { Y } & \mathrm { Z } \
\text { Ingredient A } & 3 & 2 & 4 \
\text { Ingredient B } & 2 & 3 & 1 \
\text { Ingredient C } & 1 & 0 & 2 \
\text { Ingredient D } & 6 & 8 & 4 \
\text { Cost per unit } & 0.00125 & 0.0025 & 0.015625
\end{array}$$ They must also use the following minimum quantities.
A 120, B 80, C 40, D 240
The is also a maximum of Z of 80 units.
a) Calculate how many of each product (X, Y, Z) should be produced.
b) How much is the minimized total cost?

Accepted Answer

a)
 @#IMG-DLM& b)
Mi

Question 13

If cars (C sell for $500 profit and trucks (T) sell for $300 profit which of the following represents the objective function?

Accepted Answer

A)  Maximize = 500C + 300T 
B)  Minimize = 500C + 300T 
C)  Maximize = 500C - 300T 
D)  Minimize = 300T- 500C 
E)  Minimize = 500T - 300C 
A)  Maximize = 500C + 300T 
B)  Minimize = 500C + 300T 
C)  Maximize = 500C - 300T 
D)  Minimize = 300T- 500C 
E)  Minimize = 500T - 300C

Question 14

A linear programming problem has two constraints 2X + 4Y ≥ 100 and 1X + 8Y ≤ 100, plus nonnegativity constraints on X and Y. Which of the following statements about its feasible region is true?

Accepted Answer

A)  There are four corner points including (50, 0) and (0, 12.5). 
B)  The two corner points are (0, 0) and (50, 12.5). 
C)  The graphical origin (0, 0) is in the feasible region. 
D)  The feasible region is triangular in shape, bounded by (50, 0), (33-1/3, 8-1/3), and (100, 0). 
E)  The feasible region cannot be determined without knowing whether the problem is to be minimized or maximized. 
A)  There are four corner points including (50, 0) and (0, 12.5). 
B)  The two corner points are (0, 0) and (50, 12.5). 
C)  The graphical origin (0, 0) is in the feasible region. 
D)  The feasible region is triangular in shape, bounded by (50, 0), (33-1/3, 8-1/3), and (100, 0). 
E)  The feasible region cannot be determined without knowing whether the problem is to be minimized or maximized.

Question 15

The region which satisfies all of the constraints in graphical linear programming is called the

Accepted Answer

A)  area of optimal solutions. 
B)  area of feasible solutions. 
C)  profit maximization space. 
D)  region of optimality. 
E)  region of non-negativity. 
A)  area of optimal solutions. 
B)  area of feasible solutions. 
C)  profit maximization space. 
D)  region of optimality. 
E)  region of non-negativity.

Question 16

Lost Maples Winery makes three varieties of contemporary Texas Hill Country wines: Austin Formation (a fine red), Ste. Genevieve (a table white), and Los Alamos (a hearty pink Zinfandel). The raw materials, labour, and contribution per case of each of these wines is summarized below.
 $$\begin{array} { | l | c | c | c | c | c | } 
\hline & \begin{array} { c } 
\text { Grapes } \
\text { Variety A } \
\text { bushels }
\end{array} & \begin{array} { c } 
\text { Grapes } \
\text { Variety B } \
\text { bushels }
\end{array} & \begin{array} { c } 
\text { Sugar } \
\text { pounds }
\end{array} & \begin{array} { c } 
\text { Labour (man- } \
\text { hours) }
\end{array} & \begin{array} { c } 
\text { Contrib. } \
\text { per case }
\end{array} \
\hline \text { Austin Formation } & 4 & 0 & 1 & 3 & \$ 24 \
\hline \text { Ste. Genevieve } & 0 & 4 & 0 & 1 & \$ 28 \
\hline \text { Los Alamos } & 2 & 2 & 2 & 2 & \$ 20 \
\hline
\end{array}$$ The winery has 2800 bushels of Variety A grapes, 2040 bushels of Variety B grapes, 800 pounds of sugar, and 1060 man-hours of labour available during the next week. The firm operates to achieve maximum contribution. Refer to the POM for Windows panels showing the solution to this problem. 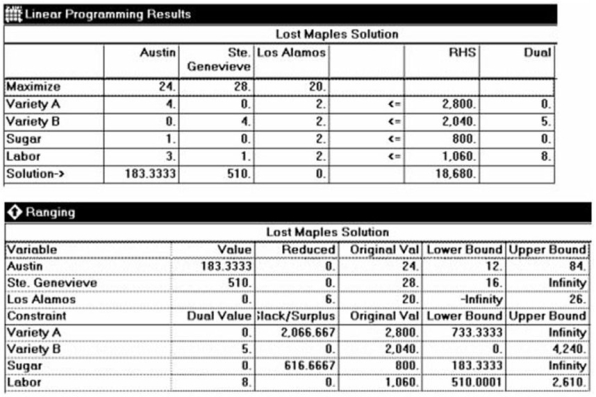  Answer the following questions.
a. For maximum contribution, how much of each wine should be produced?
b. How much contribution will be made by selling the output?
c. Is there any sugar left over? If so, how much? If not, what is its shadow price (dual value)? Explain what this value means to Lost Maples' management.
d. Interpret the meaning of the lower bound to Labour in the Ranging analysis. That is, explain how the solution would change if the amount of labour fell below that lower value.
e. Interpret the meaning of the upper bound to Los Alamos wine in the Ranging analysis.

Accepted Answer

(a) 183 1/3 cases of Austin Formation, 5

Question 17

Which of the following correctly describes all iso-profit lines for an LP maximization problem?

Accepted Answer

A)  They all pass through the origin 
B)  They are all parallel. 
C)  They all pass through the point of maximum profit. 
D)  Each line passes through at least 2 corners. 
E)  They all maximize the profit lines. 
A)  They all pass through the origin 
B)  They are all parallel. 
C)  They all pass through the point of maximum profit. 
D)  Each line passes through at least 2 corners. 
E)  They all maximize the profit lines.

Question 18

The corner-point solution method requires

Accepted Answer

A)  identifying the corner of the feasible region that has the sharpest angle. 
B)  moving the iso-profit line to the highest level that still touches some part of the feasible region. 
C)  moving the iso-profit line to the lowest level that still touches some part of the feasible region. 
D)  finding the coordinates at each corner of the feasible solution space. 
E)  none of the above. 
A)  identifying the corner of the feasible region that has the sharpest angle. 
B)  moving the iso-profit line to the highest level that still touches some part of the feasible region. 
C)  moving the iso-profit line to the lowest level that still touches some part of the feasible region. 
D)  finding the coordinates at each corner of the feasible solution space. 
E)  none of the above.

Question 19

Suppose that an iso-profit line is given to be X + Y = 15. What would be the profit made from producing 20X and 10Y?

Accepted Answer

A)  15 
B)  30 
C)  0 
D)  20X and 10Y is not a feasible solution. 
E)  Unable to determine. 
A)  15 
B)  30 
C)  0 
D)  20X and 10Y is not a feasible solution. 
E)  Unable to determine.

Question 20

A maximizing linear programming problem has two constraints: 2X + 4Y < 100 and 3X + 10Y < 210, in addition to constraints stating that both X and Y must be nonnegative. The corner points of the feasible region of this problem are

Accepted Answer

A)  (0, 0), (50, 0), (0, 21), and (20, 15). 
B)  (0, 0), (70, 0), (25, 0), and (15, 20). 
C)  (20, 15). 
D)  (0, 0), (0, 100), and (210, 0). 
E)  none of the above. 
A)  (0, 0), (50, 0), (0, 21), and (20, 15). 
B)  (0, 0), (70, 0), (25, 0), and (15, 20). 
C)  (20, 15). 
D)  (0, 0), (0, 100), and (210, 0). 
E)  none of the above.

Exam 19: Linear Programming

Two methods of solving linear programming problems by hand include the corner-point method and the ________.

In linear programming, statements such as "the blend must consist of at least 10% of ingredient A, at least 30% of ingredient B, and no more than 50% of ingredient C" can be made into valid constraints even though the percentages do not add up to 100%.

In linear programming, a statement such as "maximize contribution" becomes a(n)

In linear programming, if there are three constraints, each representing a resource that can be used up, the optimal solution must use up all of each of the three resources.

What combination of x and y will yield the optimum for this problem? Maximize $3x + $15y, subject to (1) 2x + 4y < 12 and (2) 5x + 2y < 10 and (3) x, y ≥ 0.

The region that satisfies the constraint 4X + 15Z ≥ 1000 includes the origin of the graph.

The optimal solution of a linear programming problem that consists of two variables and six constraints will probably not satisfy all six constraints as equalities.

Two methods of conducting sensitivity analysis on solved linear programming problems are ________ and ________.

A linear programming problem has two constraints 2X + 4Y ≤ 100 and 1X + 8Y ≤ 100, plus nonnegativity constraints on X and Y. Which of the following statements about its feasible region is true?

If cars (C sell for $500 profit and trucks (T) sell for $300 profit which of the following represents the objective function?

A linear programming problem has two constraints 2X + 4Y ≥ 100 and 1X + 8Y ≤ 100, plus nonnegativity constraints on X and Y. Which of the following statements about its feasible region is true?

The region which satisfies all of the constraints in graphical linear programming is called the

Which of the following correctly describes all iso-profit lines for an LP maximization problem?

The corner-point solution method requires

Suppose that an iso-profit line is given to be X + Y = 15. What would be the profit made from producing 20X and 10Y?

A maximizing linear programming problem has two constraints: 2X + 4Y < 100 and 3X + 10Y < 210, in addition to constraints stating that both X and Y must be nonnegative. The corner points of the feasible region of this problem are

Operations and Productivity

Operations Strategy in a Global Environment

Project Management

Forecasting

Design of Goods and Services

Managing Quality

Process Strategy and Sustainability

Location Strategies

Layout Strategies

Human Resources, Job Design, and Work Measurement

Supply-Chain Management

Inventory Management

Aggregate Planning

Material Requirements Planning Mrp and Erp

Short-Term Scheduling

Lean Operations

Maintenance and Reliability

Decision-Making Tools

Transportation Models

Waiting-Line Models

Learning Curves

Simulation

Supply Chain Management Analytics

Sustainability in the Supply Chain

Statistical Process Control

Capacity and Constraint Management

Filters

Two methods of conducting sensitivity analysis on solved linear programming problems are and .