Exam 19: Linear Programming
Exam 1: Operations and Productivity134 Questions
Exam 2: Operations Strategy in a Global Environment145 Questions
Exam 3: Project Management131 Questions
Exam 4: Forecasting151 Questions
Exam 5: Design of Goods and Services136 Questions
Exam 6: Managing Quality139 Questions
Exam 7: Process Strategy and Sustainability141 Questions
Exam 8: Location Strategies149 Questions
Exam 9: Layout Strategies171 Questions
Exam 10: Human Resources, Job Design, and Work Measurement202 Questions
Exam 11: Supply-Chain Management152 Questions
Exam 12: Inventory Management178 Questions
Exam 13: Aggregate Planning144 Questions
Exam 14: Material Requirements Planning Mrp and Erp184 Questions
Exam 15: Short-Term Scheduling149 Questions
Exam 16: Lean Operations147 Questions
Exam 17: Maintenance and Reliability139 Questions
Exam 18: Decision-Making Tools107 Questions
Exam 19: Linear Programming110 Questions
Exam 20: Transportation Models104 Questions
Exam 21: Waiting-Line Models145 Questions
Exam 22: Learning Curves121 Questions
Exam 23: Simulation102 Questions
Exam 24: Supply Chain Management Analytics65 Questions
Exam 25: Sustainability in the Supply Chain11 Questions
Exam 26: Statistical Process Control166 Questions
Exam 27: Capacity and Constraint Management117 Questions
Select questions type
Suppose that a maximization LP problem has corners of (0,0), (5,0), and (0,5). How many possible combinations of X and Y will yield the maximum profit if profit is given to be 5X + 5Y?
(Multiple Choice)
5.0/5  (39)
(39)
John's Locomotive Works manufactures a model locomotive. It comes in two versions-a standard (X1), and a deluxe (X2). The standard version generates $250 per locomotive for the standard version, and $350 per locomotive for the deluxe version. One constraint on John's production is labour hours. He only has 40 hours per week for assembly. The standard version requires 250 minutes each, while the deluxe requires 350 minutes. John's milling machine is also a limitation. There are only 20 hours a week available for the milling machine. The standard unit requires 60 minutes, while the deluxe requires 120. Formulate as a linear programming problem, and solve using either the graphical or corner points solution method. 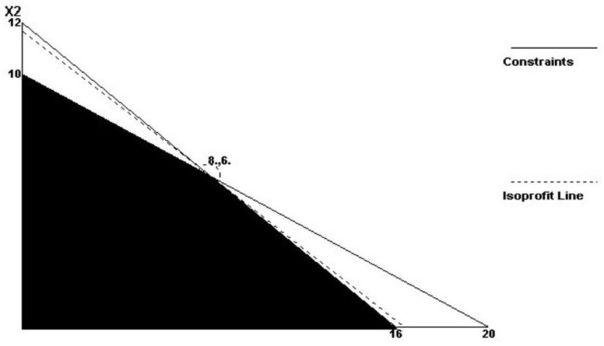
(Essay)
4.8/5  (33)
(33)
A linear programming maximization problem has been solved. In the optimal solution, two resources are scarce. If an added amount could be found for only one of these resources, how would the optimal solution be changed?
(Multiple Choice)
5.0/5  (35)
(35)
Which of the following sets of constraints results in an unbounded maximizing problem?
(Multiple Choice)
4.9/5  (36)
(36)
The feasible region in the diagram below is consistent with which one of the following constraints? 
(Multiple Choice)
4.9/5  (36)
(36)
The objective of a linear programming problem is to maximize 1.50A + 1.50B, subject to 3A + 2B ≤ 600, 2A + 4B ≤ 600, and 1A + 3B ≤ 420.
a. Plot the constraints on the grid below
b. Identify the feasible region and its corner points. Show your work.
c. What is the optimal product mix for this problem? 
(Essay)
4.7/5  (26)
(26)
A linear programming problem has three constraints: 2X + 10Y ≤ 1004X + 6Y ≤ 1206X + 3Y ≤ 90
What is the largest quantity of X that can be made without violating any of these constraints?
(Multiple Choice)
4.8/5  (33)
(33)
The difference between minimization and maximization problems is that
(Multiple Choice)
4.9/5  (37)
(37)
The region that satisfies all of the constraints in graphical linear programming is called the region of optimality.
(True/False)
4.8/5  (26)
(26)
A linear programming problem has two constraints 2X + 4Y = 100 and 1X + 8Y ≤ 100, plus non-negativity constraints on X and Y. Which of the following statements about its feasible region is true?
(Multiple Choice)
4.8/5  (38)
(38)
Tom is a habitual shopper at garage sales. Last Saturday he stopped at one where there were several types of used building materials for sale. At the low prices being asked, Tom knew that he could resell the items in another town for a substantial gain. Four things stood in his way: he could only make one round trip to resell the goods; his pickup truck bed would hold only 1000 pounds; the pickup truck bed could hold at most 70 cubic feet of merchandise; and he had only $200 cash with him. He wants to load his truck with the mix of materials that will yield the greatest profit when he resells them.
Item Cubic feet per Price per unit Weight per Can resell for Item Item 2\times4 studs 1 \ 0.10 5 pounds \ 0.80 4\times8 plywood 3 \ 0.50 20 pounds \ 3.00 Concrete blocks 0.5 \ 0.25 10 pounds \ 0.75 State the decision variables (give them labels). State the objective function. Formulate the constraints of this problem. Do not solve, but speculate on what might be a good solution for Tom. You must supply a set of quantities for the decision variables. Provide a sentence or two of support for your choice.
(Essay)
4.8/5  (26)
(26)
In which of the following has LP been applied successfully?
(Multiple Choice)
4.9/5  (37)
(37)
A company has the following usage of inputs, constraints on inputs and profit margins to make their three products.
Product Wiring Drilling Assembly Profit X202 0.6 0.41 0.8 14 Y303 0.1 0.57 0.47 9.75 Z404 0.35 0.3 0.26 12.25 There are maximum amounts of the following: 1625 hours for wiring, 1750 hours for drilling and 1175 hours for Assembly. Make sure that the units produced are integers. Solve for the above problem.
a) How many units of each product will be made?
b) What is the maximum profit?
c) Which input has the most amount of slack?
(Essay)
4.9/5  (37)
(37)
________ are restrictions that limit the degree to which a manager can pursue an objective.
(Short Answer)
5.0/5  (35)
(35)
Explain how to use the iso-profit line in a graphical maximization problem.
(Essay)
4.9/5  (38)
(38)
Suppose an LP problem was subject to constraints of
2X + Y> 10
X + 3Y> 20
Suppose that a new constraint is added, of the form 3X + A ∗ Y> 90. What is the largest value that A can have so that this new constraint is redundant?
(Essay)
4.8/5  (39)
(39)
In terms of linear programming, the fact that the solution is infeasible implies that the "profit" can increase without limit.
(True/False)
4.8/5  (35)
(35)
Showing 21 - 40 of 110
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)