Exam 15: Topics in Vector Calculus
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Use Stokes' Theorem to evaluate C 11z dx + 11x dy + 11y dz over the triangle with vertices (1, 0, 0), (0, 1, 0), and (0, 0, 1) traversed in a counterclockwise manner.
(Multiple Choice)
4.8/5  (30)
(30)
Evaluate the surface integral 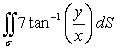 where is that portion of the paraboloid z = x2 + y2 enclosed by 1 z 9.
where is that portion of the paraboloid z = x2 + y2 enclosed by 1 z 9.
(Multiple Choice)
4.7/5  (30)
(30)
Find 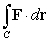 where F(x, y) = 2(2xy2 + 1)i + 4x2y j and C is the curve r(t) = e t sin t i + e t cos t j;
where F(x, y) = 2(2xy2 + 1)i + 4x2y j and C is the curve r(t) = e t sin t i + e t cos t j; 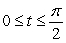 .
.
(Essay)
4.8/5  (29)
(29)
Use Green's Theorem to evaluate C 2(2xy - y2)dx + 2(x2 - y2)dy where C is the boundary of the region enclosed by y = x and y = x2. Assume that the curve c is traversed in a counterclockwise manner.
(Essay)
5.0/5  (37)
(37)
Use a line integral to find the area of the region in the first quadrant enclosed by y = 12x and y = 12x3.
(Short Answer)
4.8/5  (39)
(39)
Evaluate the surface integral 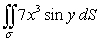 where is the surface enclosed by z = x3, 0 x 2, and 0 y .
where is the surface enclosed by z = x3, 0 x 2, and 0 y .
(Multiple Choice)
4.8/5  (33)
(33)
Sketch the vector field, F(x, y) = 4i - 8j, by drawing some typical non-intersecting vectors. The vectors need not be drawn to the same scale as the coordinate axes, but they should be in the correct proportions relative to each other.
(Essay)
4.9/5  (36)
(36)
Find the work done by the conservative force 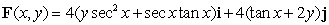 as it acts on a particle moving from P(0, 0) to
as it acts on a particle moving from P(0, 0) to 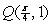 .
.
(Essay)
4.8/5  (35)
(35)
Evaluate 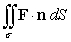 where F(x, y, z) = 2 i - z j + y k and is that portion of the paraboloid x = y2 + z2 between x = 0 and x = 4. The surface is oriented by forward unit normals.
where F(x, y, z) = 2 i - z j + y k and is that portion of the paraboloid x = y2 + z2 between x = 0 and x = 4. The surface is oriented by forward unit normals.
(Essay)
4.7/5  (31)
(31)
Evaluate 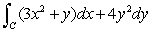 where C is the boundary of the region in the first quadrant, enclosed by the circle
where C is the boundary of the region in the first quadrant, enclosed by the circle 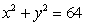 and the coordinate axes.
and the coordinate axes.
(Multiple Choice)
4.8/5  (37)
(37)
Use Stokes' Theorem to evaluate C 3(4x - 2y)dx - 3yz2dy - 3y2z dz where C is the circular region enclosed by x2 + y2 = 4, z = 2.
(Multiple Choice)
4.8/5  (31)
(31)
Use the divergence theorem to evaluate 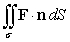 where F(x, y, z) = 2y2x i + 2yz2 j + 2x2y2 k, n is the outer unit normal to , and is the sphere x2 + y2 + z2 = 4.
where F(x, y, z) = 2y2x i + 2yz2 j + 2x2y2 k, n is the outer unit normal to , and is the sphere x2 + y2 + z2 = 4.
(Essay)
4.8/5  (44)
(44)
Use the divergence theorem to evaluate 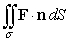 where F(x, y, z) = (x3 + 3xy2)i + z3 k, n is the outer unit normal to , and is the surface of the sphere of radius a centered at the origin.
where F(x, y, z) = (x3 + 3xy2)i + z3 k, n is the outer unit normal to , and is the surface of the sphere of radius a centered at the origin.
(Essay)
4.9/5  (34)
(34)
For F(x, y) = 3x2 i - 3y j the work done by the force field on a particle moving along an arbitrary smooth curve from P(0, 0) to Q(3, 2) is
(Multiple Choice)
4.8/5  (35)
(35)
Use the divergence theorem to evaluate 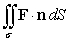 where F(x, y, z) = 4x2 i + 4y2 j + 4z2 k, n is the outer unit normal to , and is the surface of the cube enclosed by the planes 0 x 1, 0 y 1, and 0 z 1.
where F(x, y, z) = 4x2 i + 4y2 j + 4z2 k, n is the outer unit normal to , and is the surface of the cube enclosed by the planes 0 x 1, 0 y 1, and 0 z 1.
(Short Answer)
4.9/5  (35)
(35)
Find the outward flux of F(x, y, z) = 5(x - 1)i + 5(y - 3)j + 5z k across the rectangular box with vertices (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (4, 0, 0), (4, 1, 0), (4, 0, 1), and (4, 1, 1).
(Multiple Choice)
4.7/5  (33)
(33)
Use a line integral to find the area of the region enclosed by 3x2 + 12y2 = 12.
(Essay)
4.8/5  (37)
(37)
Determine whether 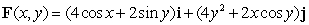 is conservative. If it is, find a potential function for it.( K is an arbitrary constant.)
is conservative. If it is, find a potential function for it.( K is an arbitrary constant.)
(Multiple Choice)
4.7/5  (30)
(30)
Showing 21 - 40 of 149
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)