Exam 15: Topics in Vector Calculus
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Use Green's Theorem to evaluate 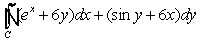 , where C is 4x2 + 9y2 = 36.
, where C is 4x2 + 9y2 = 36.
(Multiple Choice)
4.8/5  (37)
(37)
Use Green's Theorem to evaluate 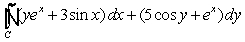 , where C is the square bounded by x = y = 0, and x = y = 1.
, where C is the square bounded by x = y = 0, and x = y = 1.
(Multiple Choice)
4.8/5  (37)
(37)
Use Stokes' Theorem to evaluate C 8z dx - 4x dy + 4x dz where C is the intersection of the cylinder x2 + y2 = 1 and the plane z = y + 1.
(Essay)
4.8/5  (31)
(31)
Use Stokes' Theorem to evaluate 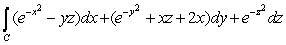 over the circle x2 + y2 = 16, z = 4.
over the circle x2 + y2 = 16, z = 4.
(Multiple Choice)
4.7/5  (30)
(30)
Use Green's Theorem to evaluate 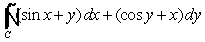 , where C is x2 + y2 = 16.
, where C is x2 + y2 = 16.
(Multiple Choice)
4.8/5  (44)
(44)
Determine whether F(x, y) = 6(y2 - 2 sin y)i + 6(2xy - 2x cos y)j is conservative. If it is, find a potential function for it.
(Essay)
4.8/5  (43)
(43)
Evaluate C 8xy dx + 4(e x + x2)dy where C is the line segment from (0, 0) to (1, 1).
(Essay)
4.9/5  (35)
(35)
Let F(x, y, z) = 8x2 i + 6y j + 3z k . Find the outward flux of the vector field F across the unit cube in the first octant and including the origin as a vertex.
(Multiple Choice)
5.0/5  (36)
(36)
Find the flux of the vector field F(x, y, z) = 3z k across the sphere x2 + y2 + z2 = 9 oriented outward.
(Multiple Choice)
4.7/5  (35)
(35)
Evaluate the surface integral 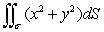 where is the portion of the cone
where is the portion of the cone 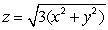 for 0 z 3.
for 0 z 3.
(Essay)
4.7/5  (33)
(33)
Use Green's Theorem to evaluate 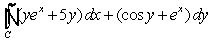 , where C is the square bounded by x = y = 0, and x = y = 1.
, where C is the square bounded by x = y = 0, and x = y = 1.
(Multiple Choice)
5.0/5  (35)
(35)
Find the outward flux of the vector field 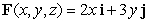 across the sphere
across the sphere 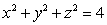 .
.
(Multiple Choice)
4.9/5  (38)
(38)
For 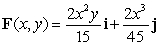 the work done by the force field on a particle moving along an arbitrary smooth curve from P(0, 0) to Q(1, 2) is
the work done by the force field on a particle moving along an arbitrary smooth curve from P(0, 0) to Q(1, 2) is
(Multiple Choice)
4.9/5  (32)
(32)
Use Green's Theorem to evaluate C -2x2y dx + 2xy2dy) where C is the boundary of the circle x2 + y2 = 16 traversed in a counterclockwise manner.
(Essay)
5.0/5  (39)
(39)
Use Stokes' Theorem to evaluate C 3(z - y)dx + 3(x - z)dy + 3(y - x)dz where C is the boundary, in the xy-plane, of the surface given by z = 4 - (x2 + y2), z 0.
(Multiple Choice)
4.7/5  (38)
(38)
Showing 101 - 120 of 149
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)