Exam 15: Topics in Vector Calculus
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Use Stokes' Theorem to evaluate 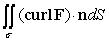 where F(x, y, z) =
where F(x, y, z) =  (z - y)i +
(z - y)i +  (z2 + x)j +
(z2 + x)j +  (x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
(x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
(Multiple Choice)
4.8/5  (38)
(38)
F (x, y, z) = 12xyz i + 12xyz j + 12xyz k. Find the outward flux of the vector field F across the cube with vertices (0, 0, 0), (0, 0, 2), (0, 2, 2), (2, 2, 2), (0, 2, 0), (2, 0, 0), (2, 2, 0), and (2, 0, 2).
(Short Answer)
4.8/5  (37)
(37)
Evaluate C 8xy dx - 8y2dy where C is the line segment from (0, 0) to (2, 1).
(Short Answer)
4.9/5  (30)
(30)
Evaluate the line integral 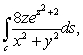 where C is the helix x = cos t, y = sin t, z = t, 0 t 2 .
where C is the helix x = cos t, y = sin t, z = t, 0 t 2 .
(Essay)
4.7/5  (31)
(31)
Use Stokes' Theorem to evaluate 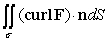 where F(x, y, z) = 11(z - y)i + 11(z2 + x)j + 11(x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
where F(x, y, z) = 11(z - y)i + 11(z2 + x)j + 11(x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
(Multiple Choice)
4.9/5  (37)
(37)
Use Green's Theorem to evaluate 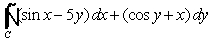 , where C is the square bounded by x = y = 0, and x = y = 1.
, where C is the square bounded by x = y = 0, and x = y = 1.
(Multiple Choice)
4.8/5  (35)
(35)
Evaluate 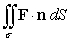 where F(x, y, z) = -x i - 2x j + (z - 1)k and is the surface enclosed by that portion of the paraboloid z = 4 - y2 which lies in the first octant and is bounded by the coordinate planes and the plane y = x. The surface is oriented by upward unit normals.
where F(x, y, z) = -x i - 2x j + (z - 1)k and is the surface enclosed by that portion of the paraboloid z = 4 - y2 which lies in the first octant and is bounded by the coordinate planes and the plane y = x. The surface is oriented by upward unit normals.
(Essay)
4.7/5  (28)
(28)
Evaluate 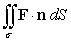 where F(x, y, z) = 9y i - 9x j - 36z2 k and is that portion of the cone
where F(x, y, z) = 9y i - 9x j - 36z2 k and is that portion of the cone 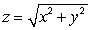 which lies above the square in the xy-plane with vertices (0, 0), (1, 0), (1, 1), and (0, 1), and oriented by downward unit normals.
which lies above the square in the xy-plane with vertices (0, 0), (1, 0), (1, 1), and (0, 1), and oriented by downward unit normals.
(Multiple Choice)
4.8/5  (44)
(44)
Use the divergence theorem to evaluate 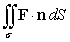 where
where 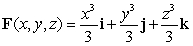 , n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 49.
, n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 49.
(Multiple Choice)
4.8/5  (30)
(30)
Let 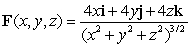 and let be a closed, orientable surface that surrounds the origin. Then the flux =
and let be a closed, orientable surface that surrounds the origin. Then the flux =
(Multiple Choice)
4.9/5  (35)
(35)
Evaluate the surface integral 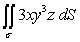 , where is the portion of the cone r(u, v) = u cos v i + u sin v j + u k for which 1 u 2,
, where is the portion of the cone r(u, v) = u cos v i + u sin v j + u k for which 1 u 2, 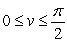 .
.
(Essay)
4.9/5  (27)
(27)
Use Stokes' Theorem to evaluate C -4yz dx + 4xz dy + 4xy dz where C is the circle x2 + y2 = 2, z = 1.
(Multiple Choice)
4.9/5  (38)
(38)
Showing 81 - 100 of 149
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)