Exam 10: Hypothesis Testing
Exam 1: An Introduction to Business Statistics and Analytics98 Questions
Exam 2: Descriptive Statistics and Analytics: Tabular and Graphical Methods120 Questions
Exam 3: Descriptive Statistics and Analytics: Numerical Methods145 Questions
Exam 4: Probability and Probability Models150 Questions
Exam 5: Predictive Analytics I: Trees, K-Nearest Neighbors, Naive Bayes,101 Questions
Exam 6: Discrete Random Variables150 Questions
Exam 7: Continuous Random Variables150 Questions
Exam 8: Sampling Distributions111 Questions
Exam 9: Confidence Intervals149 Questions
Exam 10: Hypothesis Testing150 Questions
Exam 11: Statistical Inferences Based on Two Samples140 Questions
Exam 12: Experimental Design and Analysis of Variance132 Questions
Exam 13: Chi-Square Tests120 Questions
Exam 14: Simple Linear Regression Analysis147 Questions
Exam 15: Multiple Regression and Model Building85 Questions
Exam 16: Predictive Analytics Ii: Logistic Regression, Discriminate Analysis,101 Questions
Exam 17: Time Series Forecasting and Index Numbers161 Questions
Exam 18: Nonparametric Methods103 Questions
Exam 19: Decision Theory90 Questions
Select questions type
Consider an engine parts supplier and suppose the supplier has determined that the mean and variance of the population of all cylindrical engine part outside diameters produced by the current machine are, respectively, 2.5 inches and .00075. To reduce this variance, a new machine is designed. A random sample of 20 outside diameters produced by this new machine has a sample mean of 2.5 inches and a variance of s2 = .0002 (normal distribution). In order for a cylindrical engine part to give an engine long life, the outside diameter must be between 2.43 and 2.57 inches. Find the 95 percent confidence intervals for σ2 and σ for the new machine.
Free
(Short Answer)
4.8/5  (31)
(31)
Correct Answer:
[.000116, .0004267] for σ2; [.01075, .02066] for σ.
[(19)(.0002)/32.8523, (19)(.0002)/8.90655] = [.0038/32.8523, .0038/8.90655]
= [.000116, .0004267] for σ2, [.01075, .02066] for σ.
A recent study conducted by the state government attempts to determine whether the voting public supports a further increase in cigarette taxes. The opinion poll recently sampled 1,500 voting age citizens. 1,020 of the sampled citizens were in favor of an increase in cigarette taxes. The state government would like to decide if there is enough evidence to establish whether the proportion of citizens supporting an increase in cigarette taxes is significantly greater than .66. Using the critical value rule, at α = .05, we would reject the null hypothesis.
Free
(True/False)
4.7/5  (34)
(34)
Correct Answer:
False
In testing H0: μ = 23; versus HA: μ > 23 using the critical value rule, when  = 26, s = 6, and n = 20, what is the value of the test statistic? Assume that the population from which the sample is selected is normally distributed.
= 26, s = 6, and n = 20, what is the value of the test statistic? Assume that the population from which the sample is selected is normally distributed.
Free
(Short Answer)
4.8/5  (36)
(36)
Correct Answer:
2.24
t = 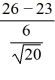 = 2.24
= 2.24
The chi-square distribution is a continuous probability distribution that is skewed to the left.
(True/False)
4.7/5  (36)
(36)
Using either the critical value rule or the p-value rule, if a one-sided null hypothesis for a single mean cannot be rejected at a given significance level, then the corresponding two-sided null hypothesis (i.e., the same sample size, the same standard deviation, and the same mean) will ________ be rejected at the same significance level.
(Multiple Choice)
4.8/5  (35)
(35)
A manufacturer of an automobile part has a process that is designed to produce the part with a target of 2.5 inches in length. In the past, the standard deviation of the length has been .035 inches. In an effort to reduce the variation in the process, the manufacturer has redesigned the process. A sample of 25 parts produced under the new process shows a sample standard deviation of .025 inches. Calculate the test statistic for testing whether the new process standard deviation has improved from the current process.
(Short Answer)
4.8/5  (30)
(30)
It is estimated that the average person in the United States uses 123 gallons of water per day. Some environmentalists believe this figure is too high and conduct a survey of 40 randomly selected Americans. They find a mean of 113.03 gallons and a population standard deviation of 25.99 gallons. Calculate the appropriate test statistic to test the hypotheses using the critical value rule.
(Short Answer)
4.9/5  (34)
(34)
A cereal manufacturer is concerned that the boxes of cereal not be underfilled or overfilled. Each box of cereal is supposed to contain 13 ounces of cereal. A random sample of 31 boxes is tested. The average weight is 12.58 ounces, and the standard deviation is .25 ounces. Calculate the test statistic to use in applying the critical value rule to test the hypotheses.
(Short Answer)
4.9/5  (41)
(41)
Failure to meet payments on student loans guaranteed by the US government has been a major problem for both banks and the government. Approximately 50 percent of all student loans guaranteed by the government are in default. A random sample of 350 loans to college students in one region of the United States indicates that 147 are in default. Calculate the appropriate test statistic to test the hypothesis that the default rate for the selected region is lower than the national percentage.
(Short Answer)
4.8/5  (36)
(36)
We are testing H0: µ ≤ 42; versus HA: µ > 42. When  = 45, s = 1.2, and n = 15, at α = .01 we do not reject the null hypothesis. Assume that the population from which the sample is selected is normally distributed.
= 45, s = 1.2, and n = 15, at α = .01 we do not reject the null hypothesis. Assume that the population from which the sample is selected is normally distributed.
(True/False)
4.8/5  (27)
(27)
When testing a null hypothesis about a single population mean and the population standard deviation is unknown, if the sample size is less than 30, one compares the computed test statistic for significance with a value from the ________ distribution.
(Multiple Choice)
4.9/5  (30)
(30)
In 1930, the average size of a public restroom was 172 square feet. By 1990, due to federal disability laws, the average size had increased to 471 square feet. Suppose that a design team believes that this standard has increased from the 1990 level. They randomly sample 23 public restrooms in a major midwestern city and obtain a mean square footage of 498.78 with a standard deviation of 46.94. Test the hypotheses at α = .001 using the critical value rule.
(Short Answer)
4.9/5  (46)
(46)
In testing H0: p = .2; versus HA: p ≠ .2 using the critical value rule, with  = .26 and n = 100, what is the value of the test statistic?
= .26 and n = 100, what is the value of the test statistic?
(Short Answer)
4.9/5  (32)
(32)
The manufacturer of an over-the-counter heartburn relief medication claims that its product brings relief in less than 3.5 minutes, on average. To be able to make this claim, the manufacturer was required by the FDA to present statistical evidence in support of the claim. The manufacturer reported that for a sample of 50 heartburn sufferers, the mean time until relief was 3.3 minutes and the population standard deviation was 1.1 minutes. Calculate the appropriate test statistic to test the hypotheses when using the critical value rule.
(Short Answer)
4.9/5  (37)
(37)
A baker must monitor the temperature at which cookies are baked. Too much variation will cause inconsistency in the texture of the cookies. Past records show that the variance of the temperatures has been 1.44 degrees. A random sample of 30 batches of cookies is selected, and the sample variance of the temperature is 4.41 degrees. Test the hypothesis that the temperature variance has increased above 1.44 degrees at α = .05.
(Short Answer)
4.9/5  (36)
(36)
Standard X-ray machines should give radiation dosages below 5.00 milliroentgens (mR). To test a certain X-ray machine, a sample of 36 observations is taken, with a mean of 4.13 mR and a population standard deviation of 1.91 mR. Calculate the p-value for this test statistic and test the claim at α = .05 using the p-value rule.
(Short Answer)
4.8/5  (32)
(32)
A null hypothesis H0: μ ≥ 2.4 is not rejected at a significance level of .04 (α = .04). The standard deviation for the normally distributed population is known to be .40. Determine the probability of a Type II error, if we assume that the actual mean is 2.125 based on a sample size of 16.
(Short Answer)
4.9/5  (33)
(33)
It has been hypothesized that on average employees spend one hour a day playing video games at work. To test this at her company, a manager takes a random sample of 35 employees, who showed a mean time of 55 minutes per day with an assumed population standard deviation of 5 minutes. What is the critical value for testing these hypotheses that the employees spend a different amount of time from one hour (60 minutes) at α = .01?
(Short Answer)
4.8/5  (35)
(35)
Showing 1 - 20 of 150
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)