Exam 17: Time Series Forecasting and Index Numbers
Exam 1: An Introduction to Business Statistics and Analytics98 Questions
Exam 2: Descriptive Statistics and Analytics: Tabular and Graphical Methods120 Questions
Exam 3: Descriptive Statistics and Analytics: Numerical Methods145 Questions
Exam 4: Probability and Probability Models150 Questions
Exam 5: Predictive Analytics I: Trees, K-Nearest Neighbors, Naive Bayes,101 Questions
Exam 6: Discrete Random Variables150 Questions
Exam 7: Continuous Random Variables150 Questions
Exam 8: Sampling Distributions111 Questions
Exam 9: Confidence Intervals149 Questions
Exam 10: Hypothesis Testing150 Questions
Exam 11: Statistical Inferences Based on Two Samples140 Questions
Exam 12: Experimental Design and Analysis of Variance132 Questions
Exam 13: Chi-Square Tests120 Questions
Exam 14: Simple Linear Regression Analysis147 Questions
Exam 15: Multiple Regression and Model Building85 Questions
Exam 16: Predictive Analytics Ii: Logistic Regression, Discriminate Analysis,101 Questions
Exam 17: Time Series Forecasting and Index Numbers161 Questions
Exam 18: Nonparametric Methods103 Questions
Exam 19: Decision Theory90 Questions
Select questions type
A restaurant has been experiencing higher sales during the weekends, compared to the weekdays. Daily restaurant sales patterns for this restaurant over a week are an example of a(n) ________ component of a time series.
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
B
The following data on prices and quantities for the years 1995 and 2000 are given for three products.
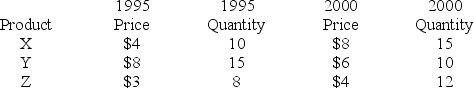 Calculate the 2000 aggregate price index.
Calculate the 2000 aggregate price index.
Free
(Short Answer)
4.8/5  (39)
(39)
Correct Answer:
120
Aggregate price index2000 = 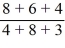 (100) = 120
(100) = 120
The purpose behind moving averages and centered moving averages is to eliminate ________.
Free
(Multiple Choice)
4.9/5  (29)
(29)
Correct Answer:
C
When using simple exponential smoothing, the value of the smoothing constant α cannot be
(Multiple Choice)
4.7/5  (34)
(34)
A positive autocorrelation implies that negative error terms will be followed by negative error terms.
(True/False)
4.9/5  (36)
(36)
Two forecasting models were used to predict the future values of a time series. The forecasts are shown below with the actual values.
 Calculate the mean squared deviation (MSD) for Model 1.
Calculate the mean squared deviation (MSD) for Model 1.
(Short Answer)
4.8/5  (40)
(40)
The Laspeyres index and the Paasche index are both examples of ________ aggregate price indexes.
(Multiple Choice)
4.8/5  (34)
(34)
Given the following data, compute the mean absolute deviation (MAD).

(Short Answer)
4.8/5  (31)
(31)
A univariate time series model is used to predict future values of a time series based only upon past values of a time series.
(True/False)
4.9/5  (37)
(37)
The smoothing constant is a number that determines how much weight is attached to each observation.
(True/False)
4.7/5  (36)
(36)
Given the following data, compute the mean absolute deviation.

(Short Answer)
4.7/5  (30)
(30)
The price and quantity of several food items are listed below for the years 1990 and 2000.
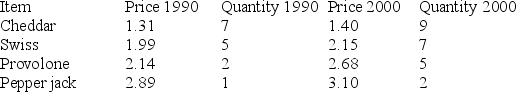 Compute the Laspeyres index, using 1990 as the base year.
Compute the Laspeyres index, using 1990 as the base year.
(Short Answer)
4.9/5  (23)
(23)
Consider the following data.
 Calculate S1 using simple exponential smoothing and α = .2.
Calculate S1 using simple exponential smoothing and α = .2.
(Short Answer)
4.9/5  (37)
(37)
Use the following price information for three grains.
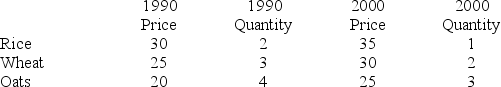 Calculate the simple price index for each grain separately.
Calculate the simple price index for each grain separately.
(Short Answer)
4.8/5  (29)
(29)
XYZ Company, Annual Data  Based on the information given in the table above, what is the MAD?
Based on the information given in the table above, what is the MAD?
(Multiple Choice)
4.8/5  (18)
(18)
Seasonal variations are periodic patterns in a time series that are repeated over time. For which one of the following time series variables is it not possible to recognize seasonal variations?
(Multiple Choice)
5.0/5  (25)
(25)
Consider the following set of quarterly sales data, given in thousands of dollars.
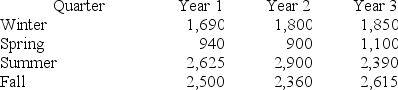 The following dummy variable model that incorporates a linear trend and constant seasonal variation was used: y(t) = β0 + β1t + βQ1(Q1) + βQ2(Q2) + βQ3(Q3) + Et. In this model, there are three binary seasonal variables (Q1, Q2, and Q3), where Qi is a binary (0,1) variable defined as:
Qi = 1, if the time series data is associated with quarter i;
Qi = 0, if the time series data is not associated with quarter i.
The results associated with this data and model are given in the following Minitab computer output.
The regression equation is
Sales = 2442 + 6.2 Time − 693 Q1 − 1499 Q2 + 153 Q3
The following dummy variable model that incorporates a linear trend and constant seasonal variation was used: y(t) = β0 + β1t + βQ1(Q1) + βQ2(Q2) + βQ3(Q3) + Et. In this model, there are three binary seasonal variables (Q1, Q2, and Q3), where Qi is a binary (0,1) variable defined as:
Qi = 1, if the time series data is associated with quarter i;
Qi = 0, if the time series data is not associated with quarter i.
The results associated with this data and model are given in the following Minitab computer output.
The regression equation is
Sales = 2442 + 6.2 Time − 693 Q1 − 1499 Q2 + 153 Q3

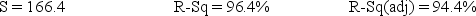 Analysis of Variance
Analysis of Variance
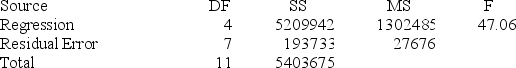 At α = .05, test the significance of the model.
At α = .05, test the significance of the model.
(Short Answer)
4.8/5  (35)
(35)
Consider the regression equation 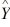 = 18.321 + 3.762(t) and the data below.
= 18.321 + 3.762(t) and the data below.
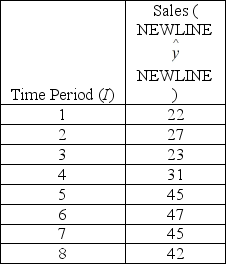 Compute the predicted value for sales for periods 6 and 7.
Compute the predicted value for sales for periods 6 and 7.
(Short Answer)
4.8/5  (36)
(36)
A simple index is obtained by dividing the current value of a time series by the value of a time series in the ________ time period and by multiplying this ratio by 100.
(Multiple Choice)
4.8/5  (41)
(41)
Assume that the current date is February 1, 2003. The linear regression model was applied to a monthly time series based on the last 24 months' sales (from January 2000 through December 2002). The following partial computer output summarizes the results.  Determine the predicted sales for this month.
Determine the predicted sales for this month.
(Multiple Choice)
4.8/5  (36)
(36)
Showing 1 - 20 of 161
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)