Exam 15: Oscillations

A lightly damped harmonic oscillator, with a damping force proportional to its speed, is oscillating with an amplitude of 0.500 cm at time t = 0. When t = 8.20 s, the amplitude has died down to 0.400 cm. At what value of t will the oscillations have an amplitude of 0.250 cm?

A 2.25-kg object is attached to a horizontal an ideal massless spring on a frictionless table. What should be the spring constant of this spring so that the maximum acceleration of the object will be g when it oscillates with amplitude of 4.50 cm?

A 56.0 kg bungee jumper jumps off a bridge and undergoes simple harmonic motion. If the period of oscillation is 11.2 s, what is the spring constant of the bungee cord, assuming it has negligible mass compared to that of the jumper?

A frictionless pendulum released from 65 degrees with the vertical will vibrate with the same frequency as if it were released from 5 degrees with the vertical because the period is independent of the amplitude and mass.

The amplitude of a lightly damped harmonic oscillator decreases from 60.0 cm to 40.0 cm in 10.0 s. What will be the amplitude of the harmonic oscillator after another 10.0 s passes?

An object is attached to a vertical ideal massless spring and bobs up and down between the two extreme points A and B. When the kinetic energy of the object is a minimum, the object is located

A 0.50-kg object is attached to an ideal massless spring of spring constant 20 N/m along a horizontal, frictionless surface. The object oscillates in simple harmonic motion and has a speed of 1.5 m/s at the equilibrium position. (a) What is the amplitude of vibration? (b) At what location are the kinetic energy and the potential energy of the system the same?

A 25 kg object is undergoing lightly damped harmonic oscillations. If the maximum displacement of the object from its equilibrium point drops to 1/3 its original value in 1.8 s, what is the value of the damping constant b?

A sewing machine needle moves up and down in simple harmonic motion with an amplitude of 1.27 cm and a frequency of 2.55 Hz. (a) What is the maximum speed of the needle? (b) What is the maximum acceleration of the needle?

If we double only the amplitude of a vibrating ideal mass-and-spring system, the mechanical energy of the system

A 0.28-kg block on a horizontal frictionless surface is attached to an ideal massless spring whose spring constant is 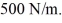The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is x = -0.052 m, find the acceleration of the block.

A 0.25 kg ideal harmonic oscillator has a total mechanical energy of 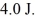If the oscillation amplitude is 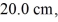what is the oscillation frequency?

A uniform meter stick is freely pivoted about the 0.20-m mark. If it is allowed to swing in a vertical plane with a small amplitude and friction, what is the frequency of its oscillations?

A large stick is pivoted about one end and allowed to swing back and forth with no friction as a physical pendulum. The mass of the stick is 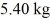and its center of gravity (found by finding its balance point) is 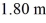from the pivot. If the period of the swinging stick is 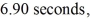what is the moment of inertia of the stick about an axis through the pivot?

Which of following graphs describes simple periodic motion with amplitude 2.00 cm and angular frequency 2.00 rad/s?

A machine part is vibrating along the x-axis in simple harmonic motion with a period of 0.27 s and a range (from the maximum in one direction to the maximum in the other) of 3.0 cm. At time t = 0 it is at its central position and moving in the +x direction. What is its position when t = 55 s?

A frictionless pendulum clock on the surface of the earth has a period of 1.00 s. On a distant planet, the length of the pendulum must be shortened slightly to have a period of 1.00 s. What is true about the acceleration due to gravity on the distant planet?

A 5.0-kg block is attached to an ideal massless spring whose spring constant is 125 N/m. The block is pulled from its equilibrium position at x = 0.00 m to a position at x = +0.687 m and is released from rest. The block then executes lightly damped oscillation along the x-axis, and the damping force is proportional to the velocity. When the block first returns to x = 0.00 m, its x component of velocity is -2.0 m/s and its x component of acceleration is +5.6 m/s². (a) What is the magnitude of the acceleration of the block upon release at x = +0.687 m. (b) Find the damping constant b.

An object is executing simple harmonic motion. What is true about the acceleration of this object? (There may be more than one correct choice.)

The position of an object that is oscillating on an ideal spring is given by the equation x = (12.3 cm) cos[(1.26s^-1)t]. At time t = 0.815 s, (a) how fast is the object moving? (b) what is the magnitude of the acceleration of the object?