Question 1

Which of the following probability distributions are associated with continuous outcomes?

Accepted Answer

A)  Poisson 
B)  Binomial 
C)  Custom 
D)  Triangular 
A)  Poisson 
B)  Binomial 
C)  Custom 
D)  Triangular

Question 2

What method is used to generate observations from a distribution?

Accepted Answer

A)  random number generator 
B)  sample generator 
C)  problem generator 
D)  steady state generator 
A)  random number generator 
B)  sample generator 
C)  problem generator 
D)  steady state generator

Question 3

What gallery distribution should be used for generating the number of times "tails" come up over 15 flips of a "fair" coin?

Accepted Answer

=PsiBinomi

Question 4

Which of the following distributions can be generated by Risk Solver Platform (RSP)?

Accepted Answer

A)  Poisson 
B)  Normal 
C)  Weibull 
D)  All of these 
A)  Poisson 
B)  Normal 
C)  Weibull 
D)  All of these

Question 5

Exhibit 12.1
The following questions use the information below.
The owner of Fix-a-dent Auto Repair wants to study the growth of his business using simulation. He is interested in simulating the number of damaged cars and the amount of damage to the cars each month. He currently repairs 100 cars per month and feels this can vary uniformly between a decrease of as much as 3% and an increase of up to 5% (average change of 1%) over the previous months. The dollar value of the damage to the cars is a normally distributed random variable with a mean of $3,000 and a standard deviation of $500. The average repair bill has been increasing steadily over the years and the owner expects the mean repair bill will increase by 1% per month. You have created the following spreadsheet to simulate the problem.
    
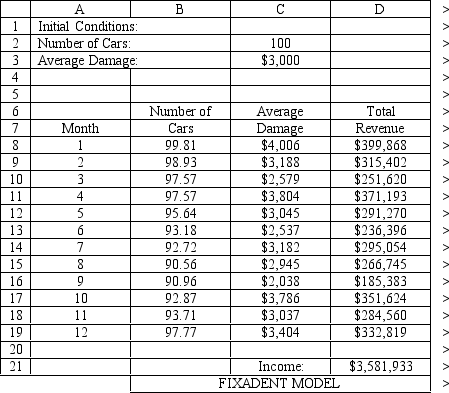
-Using the information in Exhibit 12.1, what Risk Solver Platform (RSP) function should go in cell B9 and copied to B10:B19 to compute the number of cars repaired in the subsequent months?

Accepted Answer

A)  =PsiUniform($B$8*(1+$F$2), $B$8*(1-$H$2)) 
B)  =PsiUniform(B8*(1-$F$2), B8*(1+$H$2)) 
C)  =PsiUniform($C$2*(1-$F$2), $C$2*(1+$H$2)) 
D)  =PsiIntUniform($C$2*(1-$F$2), $C$2*(1+$H$2)) 
A)  =PsiUniform($B$8*(1+$F$2), $B$8*(1-$H$2)) 
B)  =PsiUniform(B8*(1-$F$2), B8*(1+$H$2)) 
C)  =PsiUniform($C$2*(1-$F$2), $C$2*(1+$H$2)) 
D)  =PsiIntUniform($C$2*(1-$F$2), $C$2*(1+$H$2))

Question 6

Exhibit 12.2
The following questions use the information below.
The owner of Fix-a-dent Auto Repair wants to study the growth of his business using simulation. He is interested in simulating the number of damaged cars and the amount of damage to the cars each month. He currently repairs 100 cars per month and feels the change in number of cars can vary uniformly between a decrease of as much as 3% and an increase of up to 5% (average change of 1%). The dollar value of the damage to the cars is a normally distributed random variable with a mean of $3,000 and a standard deviation of $500. The average repair bill has been increasing steadily over the years and the owner expects the mean repair bill will increase by 1% per month. A spreadsheet model to simulate the problem has been run 300 times. A part of the simulation statistics output from Risk Solver Platform (RSP)and a spreadsheet for computing confidence intervals follows.
 $\begin{array}{|l|l|}
\hline {\text { Simulation Statistics }} \
\hline \text { Name } & \text { Income/Revenue } \
\hline \text { Description } & \text { Output } \
\hline \text { Cell } & \text { D21 } \
\hline \text { Minimum= } & 3339249.82 \
\hline \text { Maximum= } & 5086714.77 \
\hline \text { Mean= } & 4119518.91 \
\hline \text { Std Deviation= } & 291116.83\
\hline
\end{array}$
  
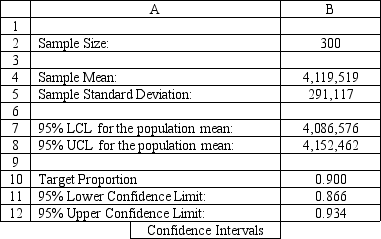-Using the information in Exhibit 12.2, what formula should go in cell B12 of the Confidence Intervals spreadsheet to compute the upper limit on a 95% confidence interval for the population proportion below 90%?

Accepted Answer

A)  =B10+1.96*B10*(1-B10)/SQRT(B2) 
B)  =B10+1.96*SQRT(B10*(1-B10)/B2) 
C)  =B10+1.96*SQRT(B10*(1-B10)*B2) 
D)  =B10+1.96*B10*(1-B10)/B2 
A)  =B10+1.96*B10*(1-B10)/SQRT(B2) 
B)  =B10+1.96*SQRT(B10*(1-B10)/B2) 
C)  =B10+1.96*SQRT(B10*(1-B10)*B2) 
D)  =B10+1.96*B10*(1-B10)/B2

Question 7

What function should be used for generating random numbers from a normal distribution with mean F1F1F1S1F1F1F10 and standard deviation F1F1F1S1F1F1F10 between the values of a and b only?

Accepted Answer

=PsiNormal(F1F1F1S1

Question 8

Best case analysis is a(n) ____ view of the problem.

Accepted Answer

A)  pessimistic 
B)  optimistic 
C)  risky 
D)  certain 
A)  pessimistic 
B)  optimistic 
C)  risky 
D)  certain

Question 9

Jim Johnson operates a bus service to take college students to "The Big City" on Friday night and bring them back to school on Sunday night. The bus has 45 seats but sometimes there are empty seats. His records show that about 5% of ticket holders do not show up for their ride. Tickets cost $20 and are non-refundable. If Jim overbooks the bus and more than 45 passengers show up, some of them will be bumped and have to miss the trip. This bumping costs the company $40 because Jim has a double-your-money back policy for bumped passengers. Jim plans to accept 48 reservations (overbook 3 seats).
 $\begin{array}{|c|c|l|c|}
\hline & \text { A } &{\text { B }} & \text { C } \
\hline 1 & &{\text { Jim's Big City Bus }} & \
\hline 2 & & \text { Reservation System } & \
\hline 3 & & & \
\hline 4 & & \text { Seats Available } & 45 \
\hline 5 & & \text { Ticket Price per Seat } & \$ 20 \
\hline 6 & & \text { Prob. of No-Show } & 0.05 \
\hline 7 & & \text { Cost of Bumping } & \$ 40 \
\hline 8 & & \text { Reservations Accepted } & 48 \
\hline 9 & & & \
\hline 10 & & \text { Passengers to Board } & 47 \
\hline 11 & & & \$ 960 \
\hline 12 & & \text { Ticket Revenue } & 0 \
\hline 13 & & \text { Opp. Cost of Empty Seats } & \$ 80 \
\hline 14 & & \text { Cost of Bumping Passengers } & \$ 880 \
\hline 15 & & \text { Marginal Profit } & \
\hline
\end{array}$
 What is Jim Johnson's expected marginal profit?

Accepted Answer

The answer of Jim Johnson operates a bus service to...

Question 10

Exhibit 12.3
The following questions use the information below.
An auto parts store wants to simulate its inventory system for engine oil. The company has collected data on the shipping time for oil and the daily demand for cases of oil. A case of oil generates a $10 profit. Customers can buy oil at any auto parts store so there are no backorders (the company loses the sale and profit). The company orders 30 cases whenever the inventory position falls below the reorder point of 15 cases. Orders are placed at the beginning of the day and delivered at the beginning of the day so the oil is available on the arrival day. An average service level of 99% is desired. The following spreadsheets have been developed for this problem. The company has simulated 2 weeks of operation for their inventory system. The current level of on-hand inventory is 25 units and no orders are pending.
      
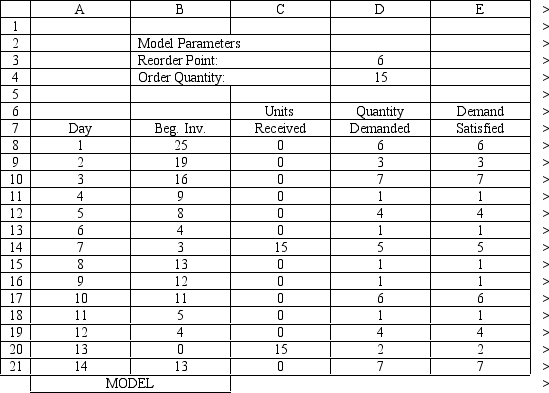
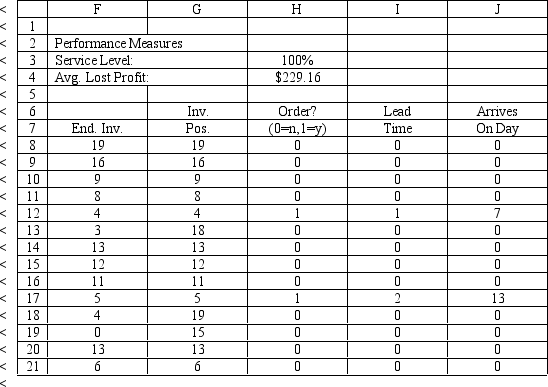
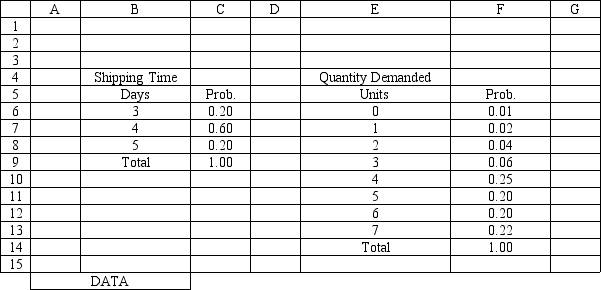-The average demand is 4.45 cases per day. Using the information in Exhibit 12.3, what formula should go in cell H4 to determine the average lost sales?

Accepted Answer

A)  =H3*4.45*10*30 
B)  =(1-H3)*4.45*10 
C)  =(1-H3)*4.45*30 
D)  =(1-H3)*4.45*10*30 
A)  =H3*4.45*10*30 
B)  =(1-H3)*4.45*10 
C)  =(1-H3)*4.45*30 
D)  =(1-H3)*4.45*10*30

Question 11

As the number of replicates in a simulation increases the width of a confidence interval computed from the simulation results will

Accepted Answer

A)  decrease. 
B)  increase. 
C)  remain the same. 
D)  change depends on standard deviation. 
A)  decrease. 
B)  increase. 
C)  remain the same. 
D)  change depends on standard deviation.

Question 12

Which of the following best describes a random variable?

Accepted Answer

A)  A spreadsheet input cell containing a random number generator. 
B)  The outcome of a simulation model. 
C)  Any variable whose value cannot be predicted with certainty. 
D)  All of these describe random variables. 
A)  A spreadsheet input cell containing a random number generator. 
B)  The outcome of a simulation model. 
C)  Any variable whose value cannot be predicted with certainty. 
D)  All of these describe random variables.

Question 13

If a spreadsheet simulation user has a probability distribution that may assume 1 of 5 values with nearly equal probability, this user has what type of distribution?

Accepted Answer

A)  A discrete distribution. 
B)  A continuous distribution. 
C)  A triangular distribution. 
D)  A normal distribution. 
A)  A discrete distribution. 
B)  A continuous distribution. 
C)  A triangular distribution. 
D)  A normal distribution.

Question 14

Which Risk Solver Platform (RSP) function will generate random integer numbers between 2 and 8?

Accepted Answer

A)  =PsiIntUniform(2, 8) 
B)  =PsiDiscrete(2, 8) 
C)  =PsiUniform(2, 8) 
D)  =PsiRandom(2, 8) 
A)  =PsiIntUniform(2, 8) 
B)  =PsiDiscrete(2, 8) 
C)  =PsiUniform(2, 8) 
D)  =PsiRandom(2, 8)

Question 15

Exhibit 12.5
The following questions use the information below.
The owner of Sal's Italian Restaurant wants to study the growth of his business using simulation. He is interested in simulating the number of customers and the amount ordered by customers each month. He currently serves 1000 customers per month and feels this can vary uniformly between a decrease of as much as 5% and an increase of up to 9%. The bill for each customer is a normally distributed random variable with a mean of $20 and a standard deviation of $5. The average order has been increasing steadily over the years and the owner expects the mean order will increase by 2% per month. You have created the following spreadsheet to simulate the problem.
    
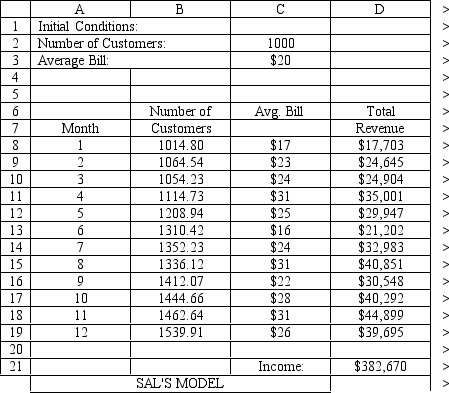
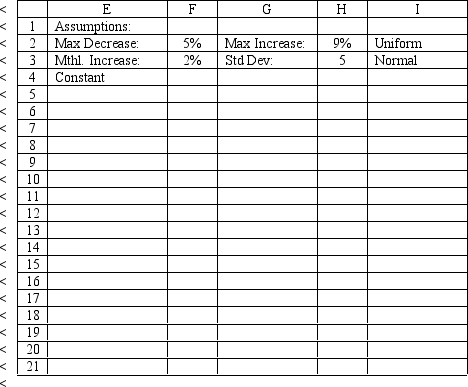-Sal, from Exhibit 12.5, has produced the following spreadsheet to compute confidence intervals on his income. What formula should go in cell B8 to compute the upper limit on a 95% confidence interval for the true population mean?
 $$\begin{array} { | c | l | c | } 
\hline &  { \text { A } } & \text { B } \
\hline 1 & & \
\hline 2 & \text { Sample Size: } & 300 \
\hline 3 & & \
\hline 4 & \text { Sample Mean: } & 309,773.56 \
\hline 5 & \text { Sample Standard Deviation: } & 33,831.44 \
\hline 6 & & \
\hline 7 & 95 \% \text { LCL far the papulation mean: } & 305,945.17 \
\hline 8 & 95 \% \text { UCL far the population mean: } & 313,601.95 \
\hline 9 & & \
\hline 10 & \text { Target Prapartion } & 0.900 \
\hline 11 & 95 \% \text { Lower Confidence Linnit: } & 0.866 \
\hline 12 & 95 \% \text { Upper Confidence I.init: } & 0.934 \
\hline
\end{array}$$

Accepted Answer

=B4+1.96*B

Question 16

Exhibit 12.2
The following questions use the information below.
The owner of Fix-a-dent Auto Repair wants to study the growth of his business using simulation. He is interested in simulating the number of damaged cars and the amount of damage to the cars each month. He currently repairs 100 cars per month and feels the change in number of cars can vary uniformly between a decrease of as much as 3% and an increase of up to 5% (average change of 1%). The dollar value of the damage to the cars is a normally distributed random variable with a mean of $3,000 and a standard deviation of $500. The average repair bill has been increasing steadily over the years and the owner expects the mean repair bill will increase by 1% per month. A spreadsheet model to simulate the problem has been run 300 times. A part of the simulation statistics output from Risk Solver Platform (RSP)and a spreadsheet for computing confidence intervals follows.
 $\begin{array}{|l|l|}
\hline {\text { Simulation Statistics }} \
\hline \text { Name } & \text { Income/Revenue } \
\hline \text { Description } & \text { Output } \
\hline \text { Cell } & \text { D21 } \
\hline \text { Minimum= } & 3339249.82 \
\hline \text { Maximum= } & 5086714.77 \
\hline \text { Mean= } & 4119518.91 \
\hline \text { Std Deviation= } & 291116.83\
\hline
\end{array}$
  
-Using the information in Exhibit 12.2, what formula should go in cell B8 of the Confidence Intervals spreadsheet to compute the upper limit on a 95% confidence interval for the true population mean?

Accepted Answer

A)  =B4+1.96*B5/SQRT(B2) 
B)  =B4+1.645*B5/SQRT(B2) 
C)  =B4-1.96*B5/SQRT(B2) 
D)  =B4+1.96*B5/B2 
A)  =B4+1.96*B5/SQRT(B2) 
B)  =B4+1.645*B5/SQRT(B2) 
C)  =B4-1.96*B5/SQRT(B2) 
D)  =B4+1.96*B5/B2

Question 17

What is the expected number of phone calls per hour based on the following distribution on the number of phone calls per hour?
 $\begin{array}{ccccc}
 & \mathrm{~A} & \mathrm{~B} & \mathrm{C} & \mathrm{D} \
1 & \text { \# of phone calls } & \mathrm{P}(\# \text { of phone calls) } & \text { \# of phone calls } & \mathrm{P}(\# \text { of phone calls) } \
2 & 1 & 0.10 & 1 & 0.10 \
2&2& 0.40 & 2 & 0.50 \
4 & 3 & 0.30 & 3 & 0.80 \
5 & 4 & 0.15 & 4 & 0.95 \
6&5 & 0.05 & 5 & 1.00
\end{array}$

Accepted Answer

(1*0.1)+(2

Question 18

Jim Johnson operates a bus service to take college students to "The Big City" on Friday night and bring them back to school on Sunday night. The bus has 45 seats but sometimes there are empty seats. His records show that about 5% of ticket holders do not show up for their ride. Tickets cost $20 and are non-refundable. If Jim overbooks the bus and more than 45 passengers show up, some of them will be bumped and have to miss the trip. This bumping costs the company $40 because Jim has a double-your-money back policy for bumped passengers. Jim wants to see what happens to profits if 48 reservations are accepted.
 $\begin{array}{|c|c|l|c|}
\hline & \text { A } & {\text { B }} & \text { C } \
\hline 1 & &{\text { Jim's Big City Bus }} & \
\hline 2 & & \text { Reservation System } & \
\hline 3 & & & \
\hline 4 & & \text { Seats Available } & 45 \
\hline 5 & & \text { Ticket Price per Seat } & \$ 20 \
\hline 6 & & \text { Prob. of No-Show } & 0.05 \
\hline 7 & & \text { Cost of Bumping } & \$ 40 \
\hline 8 & & \text { Reservations Accepted } & 48 \
\hline 9 & & & \
\hline 10 & & \text { Passengers to Board } & 47 \
\hline 11 & & & \
\hline 12 & & \text { Ticket Revenue } & \$ 960 \
\hline 13 & & \text { Opp. Cost of Empty Seats } & 0 \
\hline 14 & & \text { Cost of Bumping Passengers } & \$ 80 \
\hline 15 & & \text { Marginal Profit } & \$ 880 \
\hline
\end{array}$
 What formulas should go in cell C10 F1F1F1S1F1F1F10 C15 of the worksheet?

Accepted Answer

The answer of Jim Johnson operates a bus service to...

Question 19

Exhibit 12.1
The following questions use the information below.
The owner of Fix-a-dent Auto Repair wants to study the growth of his business using simulation. He is interested in simulating the number of damaged cars and the amount of damage to the cars each month. He currently repairs 100 cars per month and feels this can vary uniformly between a decrease of as much as 3% and an increase of up to 5% (average change of 1%) over the previous months. The dollar value of the damage to the cars is a normally distributed random variable with a mean of $3,000 and a standard deviation of $500. The average repair bill has been increasing steadily over the years and the owner expects the mean repair bill will increase by 1% per month. You have created the following spreadsheet to simulate the problem.
    
-Using the information in Exhibit 12.1, what Risk Solver Platform (RSP) function should go in cell C8 and copied to cells C9:C19 to compute the average damage per car in the month?

Accepted Answer

A)  =PsiNormal($C$3*$F$3^$A$8, $H$3) 
B)  =PsiNormal($C$3*$F$3^A8, $H$3) 
C)  =PsiNormal($C$3, $D$3*(1+$F$3)^A8) 
D)  =PsiNormal($C$3*(1+$F$3)^A8, $H$3) 
A)  =PsiNormal($C$3*$F$3^$A$8, $H$3) 
B)  =PsiNormal($C$3*$F$3^A8, $H$3) 
C)  =PsiNormal($C$3, $D$3*(1+$F$3)^A8) 
D)  =PsiNormal($C$3*(1+$F$3)^A8, $H$3)

Question 20

What function should be used for generating random integer numbers between 2 and 8?

Accepted Answer

=PsiIntUni

Which of the following probability distributions are associated with continuous outcomes?

What method is used to generate observations from a distribution?

What gallery distribution should be used for generating the number of times "tails" come up over 15 flips of a "fair" coin?

Which of the following distributions can be generated by Risk Solver Platform (RSP)?

What function should be used for generating random numbers from a normal distribution with mean  and standard deviation  between the values of a and b only?

Best case analysis is a(n) ____ view of the problem.

As the number of replicates in a simulation increases the width of a confidence interval computed from the simulation results will

Which of the following best describes a random variable?

If a spreadsheet simulation user has a probability distribution that may assume 1 of 5 values with nearly equal probability, this user has what type of distribution?

Which Risk Solver Platform (RSP) function will generate random integer numbers between 2 and 8?

What is the expected number of phone calls per hour based on the following distribution on the number of phone calls per hour? 1 \# of phone calls (\# of phone calls) \# of phone calls (\# of phone calls) 2 1 0.10 1 0.10 2 2 0.40 2 0.50 4 3 0.30 3 0.80 5 4 0.15 4 0.95 6 5 0.05 5 1.00

What function should be used for generating random integer numbers between 2 and 8?

Introduction to Modeling and Decision Analysis

Introduction to Optimization and Linear Programming

Modeling and Solving Lp Problems in a Spreadsheet

Sensitivity Analysis and the Simplex Method

Network Modeling

Integer Linear Programming

Goal Programming and Multiple Objective Optimization

Nonlinear Programming and Evolutionary Optimization

Regression Analysis

Discriminant Analysis

Time Series Forecasting

Queuing Theory

Decision Analysis

Project Management Online

Filters

Exam 12: Introduction to Simulation Using Risk Solver Platform

Which of the following probability distributions are associated with continuous outcomes?

What method is used to generate observations from a distribution?

What gallery distribution should be used for generating the number of times "tails" come up over 15 flips of a "fair" coin?

Which of the following distributions can be generated by Risk Solver Platform (RSP)?

What function should be used for generating random numbers from a normal distribution with mean  and standard deviation  between the values of a and b only?

Best case analysis is a(n) ____ view of the problem.

As the number of replicates in a simulation increases the width of a confidence interval computed from the simulation results will

Which of the following best describes a random variable?

If a spreadsheet simulation user has a probability distribution that may assume 1 of 5 values with nearly equal probability, this user has what type of distribution?

Which Risk Solver Platform (RSP) function will generate random integer numbers between 2 and 8?

What is the expected number of phone calls per hour based on the following distribution on the number of phone calls per hour? 1 \# of phone calls (\# of phone calls) \# of phone calls (\# of phone calls) 2 1 0.10 1 0.10 2 2 0.40 2 0.50 4 3 0.30 3 0.80 5 4 0.15 4 0.95 6 5 0.05 5 1.00

What function should be used for generating random integer numbers between 2 and 8?

Introduction to Modeling and Decision Analysis

Introduction to Optimization and Linear Programming

Modeling and Solving Lp Problems in a Spreadsheet

Sensitivity Analysis and the Simplex Method

Network Modeling

Integer Linear Programming

Goal Programming and Multiple Objective Optimization

Nonlinear Programming and Evolutionary Optimization

Regression Analysis

Discriminant Analysis

Time Series Forecasting

Queuing Theory

Decision Analysis

Project Management Online

Filters