Exam 11: Analytic Geometry In Three Dimensions
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
Find the general form of the equation of the plane passing through the three points.[Be sure to reduce the coefficients in your answer to lowest terms by dividing out any common factor.] (-4,4,-1), (1,6,2), (-5,-3,6)
(Multiple Choice)
4.7/5  (33)
(33)
Find symmetric equations for the line through the point and parallel to the specified line. , parallel to
x=-4-4t y=-2+2t z=1-5t
(Essay)
4.9/5  (30)
(30)
Determine the octant(s)in which (x,y,z)is located so that the conditions are satisfied. x > 0,y > 0,z > 0
(Multiple Choice)
4.7/5  (34)
(34)
A spherical building has a diameter of feet.The center of the building is placed at the origin of a three-dimensional coordinate system.What is the equation of the sphere?
(Multiple Choice)
4.8/5  (36)
(36)
Find the area of the parallelogram that has the vectors as adjacent sides. =(9,9,-11) =(9,0,11)
(Multiple Choice)
4.8/5  (39)
(39)
Find the standard form of the equation of the sphere with the given characteristics.
Center: ;diameter: 14
(Multiple Choice)
4.7/5  (41)
(41)
Determine whether u and v are parallel,orthogonal,or neither. u = ,v =
(Multiple Choice)
5.0/5  (34)
(34)
Find the magnitude of the vector described below. Initial point: (-3,7,-5)
Terminal point: (8,-3,4)
(Multiple Choice)
4.8/5  (39)
(39)
Determine whether the planes are parallel,orthogonal,or neither. 5x - y + z = -4
-x - 6y - z = -2
(Multiple Choice)
4.9/5  (37)
(37)
Find a set of parametric equations for the line through the point and parallel to the specified vector or line.(For each line,write the direction numbers as integers. )
Point: (0,0,0)
Parallel to:
(Multiple Choice)
4.8/5  (30)
(30)
Find the general form of the equation of the plane passing through the point and perpendicular to the specified vector or line.
Point: Perpendicular to:
(Multiple Choice)
4.8/5  (32)
(32)
Find the angle between the vectors.Round your answer to two decimal places. =(0,4,4) =(5,0,-6)
(Multiple Choice)
4.8/5  (37)
(37)
Find the angle of intersection of the planes in degrees.Round to a tenth of a degree.
3x + 2y - 6z = -5
-6x + 3y + z = 1
(Multiple Choice)
4.8/5  (39)
(39)
Find the angle between the two planes in degrees.Round to a tenth of a degree.
3x - 4y + z = -6
2x + y + 3z = 0
(Multiple Choice)
4.7/5  (29)
(29)
Find a set of symmetric equations for the line through the point and parallel to the specified vector or line.
Point: Parallel to:
(Multiple Choice)
4.8/5  (35)
(35)
Use the triple scalar product to find the volume of the parallelepiped having adjacent edges u,v,and w. =++5 =5+5 =5+5 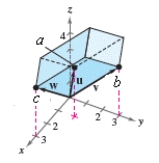
(Multiple Choice)
4.8/5  (40)
(40)
Showing 181 - 200 of 256
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)