Exam 11: Analytic Geometry In Three Dimensions
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
The brakes on a bicycle are applied by using a downward force of p pounds on the pedal when the six-inch crank makes a angle with the horizontal.Vectors representing the position of the crank and the force are and respectively.The magnitude of the torque on the crank is given by .Using the given information,write the torque T on the crank as a function of p. 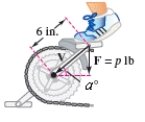
(Multiple Choice)
5.0/5  (29)
(29)
Find a set of symmetric equations for the line through the point and parallel to the specified vector or line.
Point: Parallel to:
(Multiple Choice)
4.7/5  (28)
(28)
Find the general form of the equation of the plane passing through the point and perpendicular to the specified vector or line.
Point: Perpendicular to:
(Multiple Choice)
4.8/5  (37)
(37)
The vector v and its initial point are given.Find the terminal point. v = Initial point: (-4,-8,-8)
(Multiple Choice)
4.7/5  (36)
(36)
Both the magnitude and direction of the force on a crankshaft change as the crankshaft rotates.Vectors representing the position of the crank and the force are and respectively.The magnitude of the torque on the crank is given by ,find the magnitude of the torque on the crank shaft using the position and data shown in the figure. 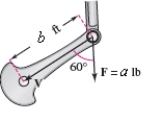
(Multiple Choice)
5.0/5  (39)
(39)
Find the general form of the equation of the plane passing through the point and perpendicular to the specified line.[Be sure to reduce the coefficients in your answer to lowest terms by dividing out any common factor.] (-7,-8,-1) x=3+2t y=-3-2t z=2+4t
(Multiple Choice)
4.8/5  (33)
(33)
Use the triple scalar product to find the volume of the parallelepiped having adjacent edges u,v,and w. =(1,1,2) =(2,2,2) =(2,0,2) 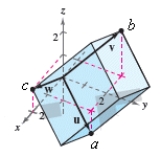
(Multiple Choice)
4.7/5  (39)
(39)
Find u × v and show that it is orthogonal to both u and v.
(Multiple Choice)
4.8/5  (37)
(37)
Find the angle between the two planes in degrees.Round to a tenth of a degree. 3x-4y+1z=-6 2x+1y-3z=0
(Multiple Choice)
4.9/5  (38)
(38)
Find the area of the parallelogram that has the vectors as adjacent sides.
(Multiple Choice)
5.0/5  (37)
(37)
Find the area of the parallelogram that has the vectors as adjacent sides. =10+6+10 =5-10+15
(Multiple Choice)
5.0/5  (28)
(28)
Find the lengths of the sides of the triangle with the indicated vertices.
(Multiple Choice)
4.8/5  (37)
(37)
Find the standard form of the equation of the sphere with the given characteristics.
Center: (-4,1,-7);radius 9
(Multiple Choice)
4.8/5  (34)
(34)
Find the standard form of the equation of the sphere with the given characteristics. Endpoints of a diameter: (-1,6,1), (7,-4,-9)
(Multiple Choice)
4.8/5  (35)
(35)
Showing 161 - 180 of 256
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)