Exam 15: Multiple Regression Model Building

TABLE 15- 8 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable, X₁ = % Attendance, X₂ = Salaries and X₃ = Spending. The coefficient of multiple determination (R ² _j) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743. The output from the best- subset regressions is given below: Adjusted Model Variables R Square R Square Std. Error 1 X1 3.05 2 0.6024 0.5936 10.5787 2 X1X2 3.66 3 0.6145 0.5970 10.5350 3 X1X2X3 4.00 4 0.6288 0.6029 10.4570 4 X1X3 2.00 3 0.6288 0.6119 10.3375 5 X2 67.35 2 0.0474 0.0262 16.3755 6 X2X3 64.30 3 0.0910 0.0497 16.1768 7 X3 62.33 2 0.0907 0.0705 15.9984 Following is the residual plot for % Attendance: Following is the output of several multiple regression models: $\text {Model (I):}$ Coefficients Std Error Stat p-value Lower 95\% Upper 95\% Intercept -753.4225 101.1149 -7.4511 2.88-09 -957.3401 -549.5050 \% Attend 8.5014 1.0771 7.8929 6.73-10 6.3292 10.6735 Salary 6.85-07 0.0006 0.0011 0.9991 -0.0013 0.0013 Spending 0.0060 0.0046 1.2879 0.2047 -0.0034 0.0153 $\text {Model (II):}$ Coefficients Standard Error t Stat p -value Intercept -753.4086 99.1451 -7.5991 1.5291-09 \% Attendance 8.5014 1.0645 7.9862 4.223-10 Spending 0.0060 0.0034 1.7676 0.0840 $\text {Model (III):}$ d f SS MS F Significance F Regression 2 8162.9429 4081.4714 39.8708 1.3201-10 Residual 44 4504.1635 102.3674 Total 46 12667.1064 Coefficients Standard Error t Stat p -value Intercept 6672.8367 3267.7349 2.0420 0.0472 \% Attendance -150.5694 69.9519 -2.1525 0.0369 \% Attendance Squared 0.8532 0.3743 2.2792 0.0276 -Referring to Table 15-8, what is the p-value of the test statistic to determine whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance?

TABLE 15- 8 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable, X₁ = % Attendance, X₂ = Salaries and X₃ = Spending. The coefficient of multiple determination (R ² _j) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743. The output from the best- subset regressions is given below: Adjusted Model Variables R Square R Square Std. 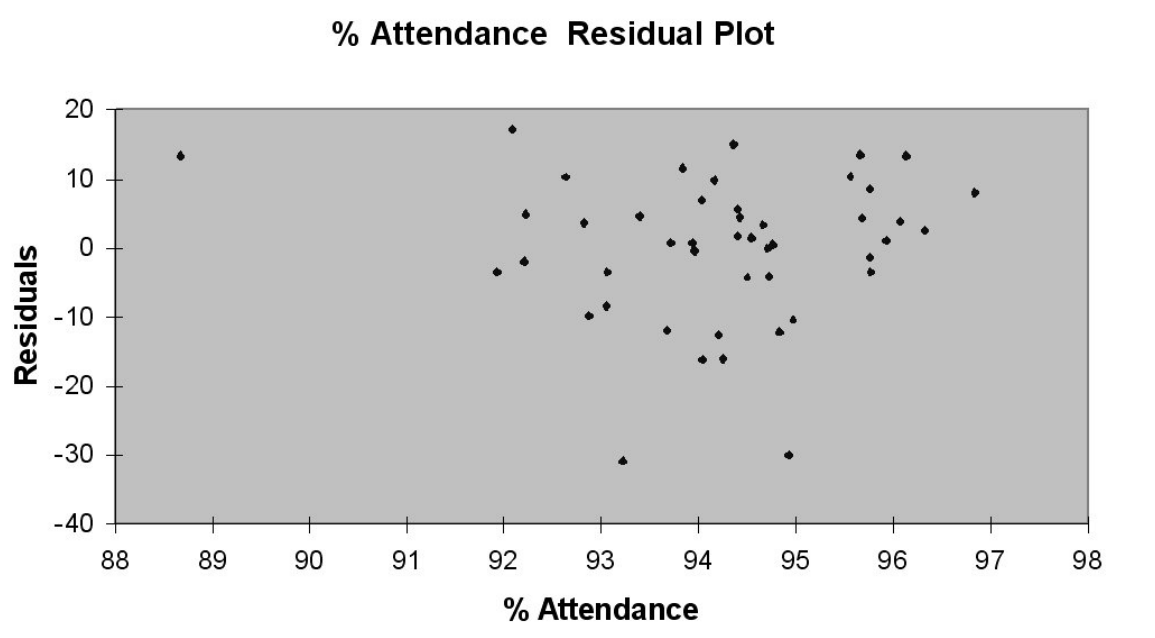Error 1 X1 3.05 2 0.6024 0.5936 10.5787 2 X1X2 3.66 3 0.6145 0.5970 10.5350 3 X1X2X3 4.00 4 0.6288 0.6029 10.4570 4 X1X3 2.00 3 0.6288 0.6119 10.3375 5 X2 67.35 2 0.0474 0.0262 16.3755 6 X2X3 64.30 3 0.0910 0.0497 16.1768 7 X3 62.33 2 0.0907 0.0705 15.9984 Following is the residual plot for % Attendance: Following is the output of several multiple regression models: $\text {Model (I):}$ Coefficients Std Error Stat p-value Lower 95\% Upper 95\% Intercept -753.4225 101.1149 -7.4511 2.88-09 -957.3401 -549.5050 \% Attend 8.5014 1.0771 7.8929 6.73-10 6.3292 10.6735 Salary 6.85-07 0.0006 0.0011 0.9991 -0.0013 0.0013 Spending 0.0060 0.0046 1.2879 0.2047 -0.0034 0.0153 $\text {Model (II):}$ Coefficients Standard Error t Stat p -value Intercept -753.4086 99.1451 -7.5991 1.5291-09 \% Attendance 8.5014 1.0645 7.9862 4.223-10 Spending 0.0060 0.0034 1.7676 0.0840 $\text {Model (III):}$ d f SS MS F Significance F Regression 2 8162.9429 4081.4714 39.8708 1.3201-10 Residual 44 4504.1635 102.3674 Total 46 12667.1064 Coefficients Standard Error t Stat p -value Intercept 6672.8367 3267.7349 2.0420 0.0472 \% Attendance -150.5694 69.9519 -2.1525 0.0369 \% Attendance Squared 0.8532 0.3743 2.2792 0.0276 -Referring to Table 15-8, which of the following predictors should first be dropped to remove collinearity?

TABLE 15-7 A chemist employed by a pharmaceutical firm has developed a muscle relaxant. She took a sample of 14 people suffering from extreme muscle constriction. She gave each a vial containing a dose (X) of the drug and recorded the time to relief (Y) measured in seconds for each. She fit a "centered" curvilinear model to this data. The results obtained by Microsoft Excel follow, where the dose (X) given has been "centered." SUMMARY OUTPUT Regression Statistics Multiple R 0.747 RSquare 0.558 Adjusted R Square 0.478 Standard Error 863.1 Observations 14 ANOVA df SS MS F Significance F Regression 2 10344797 5172399 6.94 0.0110 Residual 11 8193929 744903 Total 13 18538726 Coeff Std Error t Stut p -value Intercept 1283.0 352.0 3.65 0.0040 CenDose 25.228 8.631 2.92 0.0140 CenDoseSq 0.8604 0.3722 2.31 0.0410 -Referring to Table 15-7, suppose the chemist decides to use a t test to determine if there is a significant difference between a linear model and a curvilinear model that includes a linear term. The p-value of the test statistic for the contribution of the curvilinear term is______ .

An independent variable Xj is considered highly correlated with the other independent variables if

If a group of independent variables are not significant individually but are significant as a group at a specified level of significance, this is most likely due to

Using the Cp statistic in model building, all models with Cp c (k + 1) are equally good.

TABLE 15-9 Many factors determine the attendance at Major League Baseball games. These factors can include when the game is played, the weather, the opponent, whether or not the team is having a good season, and whether or not a marketing promotion is held. Data from 80 games of the Kansas City Royals for the following variables are collected. ATTENDANCE = Paid attendance for the game TEMP = High temperature for the day WIN% = Team's winning percentage at the time of the game OPWIN% = Opponent team's winning percentage at the time of the game WEEKEND - 1 if game played on Friday, Saturday or Sunday; 0 otherwise PROMOTION - 1 = if a promotion was held; 0 = if no promotion was held The regression results using attendance as the dependent variable and the remaining five variables as the independent variables are presented below. Regression Statistics Multiple R 0.5487 R Square 0.3011 Adjusted R Square 0.2538 Standard Error 6442.4456 Observations 80 ANOVA SS MS F Significance Regression 5 1322911703.0671 264582340.6134 6.3747 0.0001 Residual 74 3071377751.1204 41505104.7449 Total 79 4394289454.1875 Coefficients Standard Error t Stat p-value Intercept -3862.4808 6180.9452 -0.6249 0.5340 Temp 51.7031 62.9439 0.8214 0.4140 Win\% 21.1085 16.2338 1.3003 0.1975 OpWin\% 11.3453 6.4617 1.7558 0.0833 Weekend 367.5377 2786.2639 0.1319 0.8954 Promotion 6927.8820 2784.3442 2.4882 0.0151 The coefficient of multiple determination ( R ² _j ) of each of the 5 predictors with all the other remaining predictors are, respectively, 0.2675, 0.3101, 0.1038, 0.7325, and 0.7308 -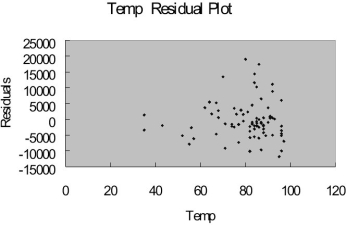Referring to Table 15-9, which of the following assumptions is most likely violated based on the residual plot for TEMP?

In multiple regression, the procedure permits variables to enter and leave the model at different stages of its development.

A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies. She proceeds to randomly select 26 large corporations and record information in millions of dollars. A statistical analyst discovers that capital spending by corporations has a significant inverse relationship with wage spending. What should the microeconomist who developed this multiple regression model be particularly concerned with?

TABLE 15- 8 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable, X₁ = % Attendance, X₂ = Salaries and X₃ = Spending. The coefficient of multiple determination (R ² _j) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743. The output from the best- subset regressions is given below: Adjusted Adjusted Model Variables R Square R Square Std. Error 1 X1 3.05 2 0.6024 0.5936 10.5787 2 X1X2 3.66 3 0.6145 0.5970 10.5350 3 X1X2X3 4.00 4 0.6288 0.6029 10.4570 4 X1X3 2.00 3 0.6288 0.6119 10.3375 5 X2 67.35 2 0.0474 0.0262 16.3755 6 X2X3 64.30 3 0.0910 0.0497 16.1768 7 X3 62.33 2 0.0907 0.0705 15.9984 Following is the residual plot for % Attendance: Following is the output of several multiple regression models: $\text {Model (I):}$ Coefficients Std Error Stat p-value Lower 95\% Upper 95\% Intercept -753.4225 101.1149 -7.4511 2.88-09 -957.3401 -549.5050 \% Attend 8.5014 1.0771 7.8929 6.73-10 6.3292 10.6735 Salary 6.85-07 0.0006 0.0011 0.9991 -0.0013 0.0013 Spending 0.0060 0.0046 1.2879 0.2047 -0.0034 0.0153 $\text {Model (II):}$ Coefficients Standard Error t Stat p -value Intercept -753.4086 99.1451 -7.5991 1.5291-09 \% Attendance 8.5014 1.0645 7.9862 4.223-10 Spending 0.0060 0.0034 1.7676 0.0840 $\text {Model (III):}$ d f SS MS F Significance F Regression 2 8162.9429 4081.4714 39.8708 1.3201-10 Residual 44 4504.1635 102.3674 Total 46 12667.1064 Coefficients Standard Error t Stat p -value Intercept 6672.8367 3267.7349 2.0420 0.0472 \% Attendance -150.5694 69.9519 -2.1525 0.0369 \% Attendance Squared 0.8532 0.3743 2.2792 0.0276 -Referring to Table 15-8, the "best" model chosen using the adjusted R-square statistic is

Which of the following is not used to find a "best" model?

TABLE 15-4 In Hawaii, condemnation proceedings are under way to enable private citizens to own the property that their homes are built on. Until recently, only estates were permitted to own land, and homeowners leased the land from the estate. In order to comply with the new law, a large Hawaiian estate wants to use regression analysis to estimate the fair market value of the land. The following model was fit to data collected for n = 20 properties, 10 of which are located near a cove. Model 1: $Y=\beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\beta_{3} X_{1} X_{2}+\beta_{4} X_{1}^{2}+\beta_{5} X_{1}^{2} X_{2}+\varepsilon$ where Y = Sale price of property in thousands of dollars X₁ = Size of property in thousands of square feet X₂ = 1 if property located near cove, 0 if not Using the data collected for the 20 properties, the following partial output obtained from Microsoft Excel is shown: SUMMARY OUTPUT Regression Statistics Multiple R 0.985 R Square 0.970 Standard Error 9.5 Observations 20 ANOVA df SS MS F Significance F Regression 5 28324 5664 62.2 0.0001 Residual 14 1279 91 Total 19 29063 Coeff STd Error t Stut p -value Intercept -32.1 35.7 -0.90 0.3834 Size 122 5.9 2.05 0.0594 Cove -104.3 53.5 -1.95 0.0715 Size Cove 17.0 8.5 1.99 0.0661 SizeSq -0.3 0.2 -1.28 0.2204 SizeSq Cove -0.3 0.3 -1.13 0.2749 -Referring to Table 15-4, is the overall model statistically adequate at a 0.05 level of significance for predicting sale price (Y)?

TABLE 15- 8 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable, X₁ = % Attendance, X₂ = Salaries and X₃ = Spending. The coefficient of multiple determination (R ² _j) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743. The output from the best- subset regressions is given below: Adjusted Model Variables R Square R Square Std. Error 1 X1 3.05 2 0.6024 0.5936 10.5787 2 X1X2 3.66 3 0.6145 0.5970 10.5350 3 X1X2X3 4.00 4 0.6288 0.6029 10.4570 4 X1X3 2.00 3 0.6288 0.6119 10.3375 5 X2 67.35 2 0.0474 0.0262 16.3755 6 X2X3 64.30 3 0.0910 0.0497 16.1768 7 X3 62.33 2 0.0907 0.0705 15.9984 Following is the residual plot for % Attendance: Following is the output of several multiple regression models: $\text {Model (I):}$ Coefficients Std Error Stat p-value Lower 95\% Upper 95\% Intercept -753.4225 101.1149 -7.4511 2.88-09 -957.3401 -549.5050 \% Attend 8.5014 1.0771 7.8929 6.73-10 6.3292 10.6735 Salary 6.85-07 0.0006 0.0011 0.9991 -0.0013 0.0013 Spending 0.0060 0.0046 1.2879 0.2047 -0.0034 0.0153 $\text {Model (II):}$ Coefficients Standard Error t Stat p -value Intercept -753.4086 99.1451 -7.5991 1.5291-09 \% Attendance 8.5014 1.0645 7.9862 4.223-10 Spending 0.0060 0.0034 1.7676 0.0840 $\text {Model (III):}$ d f SS MS F Significance F Regression 2 8162.9429 4081.4714 39.8708 1.3201-10 Residual 44 4504.1635 102.3674 Total 46 12667.1064 Coefficients Standard Error t Stat p -value Intercept 6672.8367 3267.7349 2.0420 0.0472 \% Attendance -150.5694 69.9519 -2.1525 0.0369 \% Attendance Squared 0.8532 0.3743 2.2792 0.0276 -Referring to Table 15-8, the residual plot suggests that a nonlinear model on % attendance may be a better model.

TABLE 15-3 A certain type of rare gem serves as a status symbol for many of its owners. In theory, for low prices, the demand increases and it decreases as the price of the gem increases. However, experts hypothesize that when the gem is valued at very high prices, the demand increases with price due to the status owners believe they gain in obtaining the gem. Thus, the model proposed to best explain the demand for the gem by its price is the quadratic model: $Y=\beta_{0}+\beta_{1} X+\beta_{2} X^{2}+\varepsilon$ where Y = demand (in thousands) and X = retail price per carat. This model was fit to data collected for a sample of 12 rare gems of this type. A portion of the computer analysis obtained from Microsoft Excel is shown below: SUMMARY OUTPUT Regression Statistics Multiple R 0.994 R Square 0.988 Standard Error 12.42 Observations 12 $\text { ANOVA }$ df SS MS F Signifcance F Regression 2 115145 57573 373 0.0001 Residual 9 1388 154 Total 11 116533 Coeff Std Error t Stat p-value Intercept 286.42 9.66 29.64 0.0001 Price -0.31 0.06 -5.14 0.0006 Frice Sq 0.000067 0.00007 0.95 0.3647 -Referring to Table 15-3, what is the value of the test statistic for testing whether there is an upward curvature in the response curve relating the demand (Y) and the price (X)?

TABLE 15-9 Many factors determine the attendance at Major League Baseball games. These factors can include when the game is played, the weather, the opponent, whether or not the team is having a good season, and whether or not a marketing promotion is held. Data from 80 games of the Kansas City Royals for the following variables are collected. ATTENDANCE = Paid attendance for the game TEMP = High temperature for the day WIN% = Team's winning percentage at the time of the game OPWIN% = Opponent team's winning percentage at the time of the game WEEKEND - 1 if game played on Friday, Saturday or Sunday; 0 otherwise PROMOTION - 1 = if a promotion was held; 0 = if no promotion was held The regression results using attendance as the dependent variable and the remaining five variables as the independent variables are presented below. Regression Statistics Multiple R 0.5487 R Square 0.3011 Adjusted R Square 0.2538 Standard Error 6442.4456 Observations 80 ANOVA SS MS F Significance Regression 5 1322911703.0671 264582340.6134 6.3747 0.0001 Residual 74 3071377751.1204 41505104.7449 Total 79 4394289454.1875 Coefficients Standard Error t Stat p-value Intercept -3862.4808 6180.9452 -0.6249 0.5340 Temp 51.7031 62.9439 0.8214 0.4140 Win\% 21.1085 16.2338 1.3003 0.1975 OpWin\% 11.3453 6.4617 1.7558 0.0833 Weekend 367.5377 2786.2639 0.1319 0.8954 Promotion 6927.8820 2784.3442 2.4882 0.0151 The coefficient of multiple determination ( R ² _j ) of each of the 5 predictors with all the other remaining predictors are, respectively, 0.2675, 0.3101, 0.1038, 0.7325, and 0.7308. -Referring to Table 15-9, what is the value of the test statistic to determine whether TEMP makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance?

The parameter estimates are biased when collinearity is present in a multiple regression equation.

TABLE 15-7 A chemist employed by a pharmaceutical firm has developed a muscle relaxant. She took a sample of 14 people suffering from extreme muscle constriction. She gave each a vial containing a dose (X) of the drug and recorded the time to relief (Y) measured in seconds for each. She fit a "centered" curvilinear model to this data. The results obtained by Microsoft Excel follow, where the dose (X) given has been "centered." SUMMARY OUTPUT Regression Statistics Multiple R 0.747 RSquare 0.558 Adjusted R Square 0.478 Standard Error 863.1 Observations 14 ANOVA df SS MS F Significance F Regression 2 10344797 5172399 6.94 0.0110 Residual 11 8193929 744903 Total 13 18538726 Coeff Std Error t Stut p -value Intercept 1283.0 352.0 3.65 0.0040 CenDose 25.228 8.631 2.92 0.0140 CenDoseSq 0.8604 0.3722 2.31 0.0410 -Referring to Table 15-7, suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose. If she chooses to use a level of significance of 0.01 she would decide that there is a significant curvilinear relationship.

In data mining where huge data sets are being explored to discover relationships among a large number of variables, the best-subsets approach is more practical than the stepwise regression approach.

Using the hat matrix elements hi to determine influential points in a multiple regression model with k independent variable and n observations, X_i is an influential point if

The logarithm transformation can be used