Exam 13: Simple Linear Regression

TABLE 13- 11 A company that has the distribution rights to home video sales of previously released movies would like to use the box office gross (in millions of dollars) to estimate the number of units (in thousands of units) that it can expect to sell. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different movie titles: Regression Statistics Multiple R 0.8531 R Square 0.7278 AdjustedR Square 0.7180 StandardError 47.8668 Observations 30 ANOVA d f SS MS F Significance F Regression 1 171499.78 171499.78 74.8505 2.1259E-09 Residual 28 64154.42 2291.23 Total 29 235654.20 Coefficients Standard Error t Stat p -value Lower 95\% Upper 95\% Intercept 76.5351 11.8318 6.4686 5.24-07 52.2987 100.7716 Gross 4.3331 0.5008 8.6516 2.13-09 3.3072 5.3590 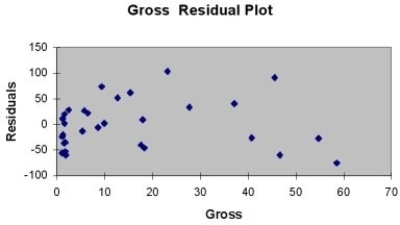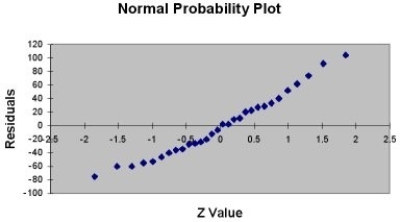-Referring to Table 13-11, what is the standard error of estimate?

TABLE 13-4 The managers of a brokerage firm are interested in finding out if the number of new clients a broker brings intothe firm affects the sales generated by the broker. Theysample 12 brokersand determine the numberof new clients they have enrolled in the last year and their sales amountsin thousandsof dollars. These data are presented in the table that follows. Broker Clients Sales 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Table 13-3, suppose the director of cooperative education wants to obtain a 95% prediction interval estimate for the number of job offers received by people who have had exactly one cooperative education job. The prediction interval is from_____ to_____ .

TABLE 13-4 The managers of a brokerage firm are interested in finding out if the number of new clients a broker brings intothe firm affects the sales generated by the broker. Theysample 12 brokersand determine the numberof new clients they have enrolled in the last year and their sales amountsin thousandsof dollars. These data are presented in the table that follows. Broker Clients Sales 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Table 13-4, the managers of the brokerage firm wanted to test the hypothesis that the number of new clients brought in had a positive impact on the amount of sales generated. For a test with a level of significance of 0.01, the null hypothesis should be rejected if the value of the test statistic is ______ .

TABLE 13- 11 A company that has the distribution rights to home video sales of previously released movies would like to use the box office gross (in millions of dollars) to estimate the number of units (in thousands of units) that it can expect to sell. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different movie titles: Regression Stadistics Multiple R 0.8531 R Square 0.7278 Adjusted R Square 0.7180 Standard Error 47.8668 Observations 30 ANOVA d f SS MS F Significance F Regression 1 171499.78 171499.78 74.8505 2.1259E-09 Residual 28 64154.42 2291.23 Total 29 235654.20 Coefficients Standard Error t Stat p -value Lower 95\% Upper 95\% Intercept 76.5351 11.8318 6.4686 5.24-07 52.2987 100.7716 Gross 4.3331 0.5008 8.6516 2.13-09 3.3072 5.3590 -Referring to Table 13-11, what is the standard deviation around the regression line?

TABLE 13- 11 A company that has the distribution rights to home video sales of previously released movies would like to use the box office gross (in millions of dollars) to estimate the number of units (in thousands of units) that it can expect to sell. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different movie titles: Regression Statistics Multiple R 0.8531 RSquare 0.7278 Adjusted R Square 0.7180 Standard Error 47.8668 Observations 30 ANOVA d f SS MS F Significance F Regression 1 171499.78 171499.78 74.8505 2.1259E-09 Residual 28 64154.42 2291.23 Total 29 235654.20 Coefficients Standard Error t Stat p -value Lower 95\% Upper 95\% Intercept 76.5351 11.8318 6.4686 5.24-07 52.2987 100.7716 Gross 4.3331 0.5008 8.6516 2.13-09 3.3072 5.3590 -Referring to Table 13-11, which of the following is the correct interpretation for the slope coefficient?

TABLE 13-10 The management of a chain electronic store would like to develop a model for predicting the weekly sales (in thousand of dollars) for individual stores based on the number of customers who made purchases. A random sample of 12 stores yields the following results: Customers Sales (Thousands of Dollars) 907 11.20 926 11.05 713 8.21 741 9.21 780 9.42 898 10.08 510 6.73 529 7.02 460 6.12 872 9.52 650 7.53 603 7.25 -Referring to Table 13-10, which is the correct null hypothesis for testing whether the number of customers who make purchase affects weekly sales?

TABLE 13-6 The following EXCEL tables are obtained when "Score received on an exam (measured in percentage points)" (Y) is regressed on "percentage attendance" (X) for 22 students in a Statistics for Business and Economics course. Regression Statistics Multiple R 0.142620229 R Square 0.02034053 Adjusted R Square -0.028642444 Standard Error 20.25979924 Observations 22 Coefficients Standard Enor T Stat p -value Intercept 39.39027309 37.24347659 1.057642216 0.302826622 Attendance 0.340583573 0.52852452 0.644404489 0.526635689 -Referring to Table 13-6, which of the following statements is true?

TABLE 13-4 The managers of a brokerage firm are interested in finding out if the number of new clients a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new clients they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. Broker Cliente Sales 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Table 13-4, the managers of the brokerage firm wanted to test the hypothesis that the true slope was equal to 0. At a level of significance of 0.01, the null hypothesis should be_____ (accepted or rejected).

If the Durbin-Watson statistic has a value close to 4, which assumption is violated?

TABLE 13-5 The managing partner of an advertising agency believes that his company's sales are related to the industry sales. He uses Microsoft Excel's Data Analysis tool to analyze the last 4 years of quarterly data with the following results: Regression Statistics Multiple R 0.802 R Square 0.643 Adjusted R Square 0.618 Standard Error SYX 0.9224 Observations 16 ANOVA d f SS MS F Sig.F Regression 1 21.497 21.497 25.27 0.000 Error 14 11.912 0.851 Total 15 33.409 Predictor Coefficients Standard Error t Stat p -value Intercept 3.962 1.440 2.75 0.016 Industry 0.040451 0.008048 5.03 0.000 -Referring to Table 13-5, the estimates of the Y-intercept and slope are and_____, _____respectively.

The least squares method minimizes which of the following?

Testing for the existence of correlation is equivalent to

TABLE 13-2 A candy bar manufacturer is interested in trying to estimate how sales are influenced by the price of their product. To do this, the company randomly chooses 6 small cities and offers the candy bar at different prices. Using candy bar sales as the dependent variable, the company will conduct a simple linear regression on the data below: City Price (\ ) Sales River Falls 1.30 100 Hudson 1.60 90 Ellsworth 1.80 90 Prescott 2.00 40 Rock Elm 2.40 38 Stillwater 2.90 32 -Referring to Table 13-2, if the price of the candy bar is set at $2, the estimated average sales will be

TABLE 13- 11 A company that has the distribution rights to home video sales of previously released movies would like to use the box office gross (in millions of dollars) to estimate the number of units (in thousands of units) that it can expect to sell. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different movie titles: Regression Statistics Multiple R 0.8531 R Square 0.7278 Adjusted R Square 0.7180 Standard Error 47.8668 Observations 30 ANOVA d f SS MS F Significance F Regression 1 171499.78 171499.78 74.8505 2.1259E-09 Residual 28 64154.42 2291.23 Total 29 235654.20 Coefficients Standard Error t Stat p -value Lower 95\% Upper 95\% Intercept 76.5351 11.8318 6.4686 5.24-07 52.2987 100.7716 Gross 4.3331 0.5008 8.6516 2.13-09 3.3072 5.3590 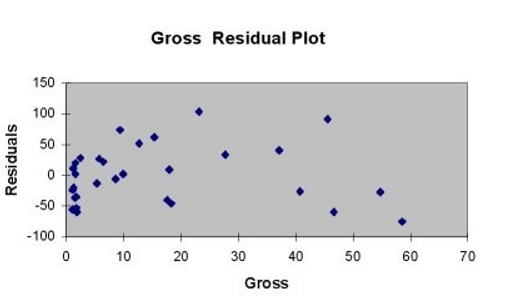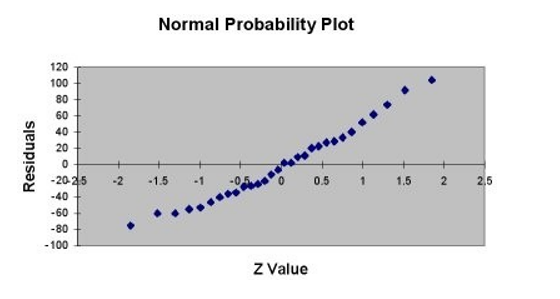-Referring to Table 13-11, which of the following is the correct alternative hypothesis for testing whether there is a linear relationship between box office gross and home video unit sales?

TABLE 13-5 The managing partner of an advertising agency believes that his company's sales are related to the industry sales. He uses Microsoft Excel's Data Analysis tool to analyze the last 4 years of quarterly data with the following results: Regression Statistics Multiple R 0.802 R Square 0.643 Adjusted R Square 0.618 Standard Error SYX 0.9224 Observations 16 ANOVA d f SS MS F Sig.F Regression 1 21.497 21.497 25.27 0.000 Error 14 11.912 0.851 Total 15 33.409 Predictor Coefficients Standard Error t Stat p -value Intercept 3.962 1.440 2.75 0.016 Industry 0.040451 0.008048 5.03 0.000 -Referring to Table 13-5, the correlation coefficient is______ .

The Durbin-Watson D statistic is used to check the assumption of normality.

TABLE 13-5 The managing partner of an advertising agency believes that his company's sales are related to the industry sales. He uses Microsoft Excel's Data Analysis tool to analyze the last 4 years of quarterly data with the following results: Regression Statistics Multiple R 0.802 R Square 0.643 Adjusted R Square 0.618 Standard Error SYX 0.9224 Observations 16 ANOVA df SS MS F Sig.F Regression 1 21.497 21.497 25.27 0.000 Error 14 11.912 0.851 Total 15 33.409 Predictor Coeffcients Standard Error Stat p-value Intercept 3.962 1.440 2.75 0.016 Industry 0.040451 0.008048 5.03 0.000 Durbin- Watson Statistic 1.59 -Referring to Table 13-5, the prediction for a quarter in which X = 120 is Y = ________.

TABLE 13-10 The management of a chain electronic store would like to develop a model for predicting the weekly sales (in thousand of dollars) for individual stores based on the number of customers who made purchases. A random sample of 12 stores yields the following results: Customers Sales (Thousands of Dollars) 907 11.20 926 11.05 713 8.21 741 9.21 780 9.42 898 10.08 510 6.73 529 7.02 460 6.12 872 9.52 650 7.53 603 7.25 -Referring to Table 13-10, what is the value of the coefficient of correlation?

A zero population correlation coefficient between a pair of random variables means that there is no linear relationship between the random variables.

TABLE 13-3 The director of cooperative education at a state college wants to examine the effect of cooperative education job experience on marketability in the work place. She takes a random sample of 4 students. For these 4, she finds out how many times each had a cooperative education job and how many job offers they received upon graduation. These data are presented in the table below. Student CoopJobs JobOffer 1 1 4 2 2 6 3 1 3 4 0 1 -Referring to Table 13-3, suppose the director of cooperative education wants to obtain a 95% prediction interval for the number of job offers received by a person who has had exactly two cooperative education jobs. The t critical value she would use is_____ .