Exam 9: Hypothesis Testing

The local pharmacy prides itself on the accuracy of the number of tablets that are dispensed in a 60-count prescription.The new manager feels that the pharmacy assistants might have become careless in counting due to an increase in the volume of prescriptions.To test her theory,she randomly selects 40 prescriptions requiring 60 tablets and recounts the number in each bottle.She finds a sample mean of 62.05 and a standard deviation of 4.45.Calculate the test statistic for testing that the number of tablets is significantly different from 60.

A test statistic is computed from sample data in hypothesis testing and is used in making a decision about whether or not to reject the null hypothesis.

Last year,TV station KAAA had a share of the 6 p.m.news audience approximately equal to,but not greater than,25 percent.The advertising department for the station believes the current audience share is higher than the 25 percent share they had last year.In an attempt to substantiate this belief,the station surveyed a random sample of 400 viewers of 6 p.m.news and found that 146 watched KAAA.Test these hypotheses at α = .001 using the critical value.

Consider an engine parts supplier,and suppose the supplier has determined that the mean and variance of the population of all cylindrical engine part outside diameters produced by the current machine are,respectively,2.5 inches and .00075.To reduce this variance,a new machine is designed.A random sample of 20 outside diameters produced by this new machine has a sample mean of 2.5 inches,a variance of s² = .0002 (normal distribution).In order for a cylindrical engine part to give an engine long life,the outside diameter must be between 2.43 and 2.57 inches.Find the 95 percent confidence intervals for σ² and σ for the new machine.

In order to make statistical inferences about σ² that are valid using a chi-square distribution,the assumption is that the sampled population is also a chi-square distribution.

A mail-order business prides itself in its ability to fill customers' orders in less than six calendar days,on average.Periodically,the operations manager selects a random sample of customer orders and determines the number of days required to fill the orders.On one occasion when a sample of 39 orders was selected,the average number of days was 6.65 with a population standard deviation of 1.5 days.Calculate the appropriate test statistic to test the hypotheses.

Failure to meet payments on student loans guaranteed by the US government has been a major problem for both banks and the government.Approximately 50 percent of all student loans guaranteed by the government are in default.A random sample of 350 loans to college students in one region of the United States indicates that 147 are in default.Calculate the appropriate test statistic to test the hypothesis that the default rate for the selected region is lower than the national percentage.

Determine the p-value for H₀: p ≤ .5;versus H_A: p> .5,when n = 225 and 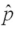= .54.

Based on a random sample of 25 units of product X,the average weight is 102 lbs.and the sample standard deviation is 10 lbs.We would like to decide whether there is enough evidence to establish that the average weight for the population of product X is greater than 100 lbs.Assume the population is normally distributed.What is the value of the test statistic to test the claim?

For a fixed sample size,the lower we set α,the higher is the ___________.

The manager of a grocery store wants to determine whether the amount of water contained in 1-gallon bottles purchased from a nationally known manufacturer actually average 1 gallon.It is known from the specifications that the standard deviation of the amount of water is equal to 0.02 gallon.A random sample of 32 bottles is selected,and the mean amount of water per 1-gallon bottle is found to be 0.995 gallon.Calculate the p-value and test whether the specifications are being met at α = .001.

As the Type II error β of a statistical test increases,the power of the test _____________.

The rejection of a true null hypothesis is called a ______________ error.

We are testing H₀: μ = 32;versus H_A: μ > 32.If 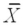= 36,s = 1.6,and n = 30,at α = .05,we should reject H₀.

The ____________ hypothesis will be accepted only if there is convincing sample evidence that it is true.

A sample of 400 journalism majors at a major research university was asked if they agreed with the following statement: Government should be more involved in oversight and regulation of reporting. Fifty-two percent of the respondents agreed with the statement.Calculate the p-value associated with the test statistic and test at α = .05.

In testing H₀: p = .2;versus H_A: p ≠ .2,with 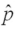= .26 and n = 100,what is the value of the test statistic?

Consider an engine parts supplier,and suppose the supplier has determined that the mean and variance of the population of all cylindrical engine part outside diameters produced by the current machine are,respectively,2.5 inches and .00075.To reduce this variance,a new machine is designed.A random sample of 20 outside diameters produced by this new machine has a sample mean of 2.5 inches and a variance of s² = .0002 (normal distribution).In order for a cylindrical engine part to give an engine long life,the outside diameter must be between 2.43 and 2.57 inches.If σ² denotes the variance of the population of all outside diameters that would be produced by the new machine,test H₀: σ² = .00075 versus H_a: σ²< .00075 by setting α = .05.

When testing a null hypothesis about a single population mean and the population standard deviation is unknown,if the sample size is less than 30,one compares the computed test statistic for significance with a value from the ___________ distribution.

When the null hypothesis is not rejected,there is no possibility of making a Type I error.