Exam 9: Hypothesis Testing

A null hypothesis H₀: μ ≥ 2.4 is not rejected at a significance level of 0.04.(α = 0.04).The standard deviation for the normally distributed population is known to be 0.40.Determine the Type II error,if we assume that the actual mean is 2.125 based on a sample size of 16.

When the null hypothesis is true,there is no possibility of making a Type I error.

A manufacturer of an automobile part has a process that is designed to produce the part with a target of 2.5 inches in length.In the past,the standard deviation of the length has been 0.035 inches.In an effort to reduce the variation in the process,the manufacturer has redesigned the process.A sample of 25 parts produced under the new process shows a sample standard deviation of 0.025 inches.Calculate the test statistic for testing whether the new process standard deviation has improved from the current process.

As the level of significance α increases,we are more likely to reject the null hypothesis.

We test H₀: μ ≤ 3.0;versus H_A: μ > 3.0.If 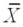= 3.44,s = .57,and n = 13,at a significance level of .05,we do not reject H₀.(Assume population normality. )

Based on a random sample of 25 units of product X,the average weight is 102 lbs. ,and the sample standard deviation is 10 lbs.We would like to decide if there is enough evidence to establish that the average weight for the population of product X is greater than 100 lbs.Assume the population is normally distributed.At α = .01,we can reject the null hypothesis.

The local pharmacy prides itself on the accuracy of the number of tablets that are dispensed in a 60-count prescription.The new manager feels that the pharmacy assistants might have become careless in counting due to an increase in the volume of prescriptions.To test her theory,she randomly selects 40 prescriptions requiring 60 tablets and recounts the number in each bottle.She finds a sample mean of 61.35.Assume a population standard deviation of 4.45.If we want the probability of a Type I error and Type II error to be equal to .05,what is the sample size needed to make both the probability of a Type I error and the probability of a Type II error as small as possible.(Assume an alternative value of the population mean of 61. )The claim is that the tablet count is different from 60.

The null hypothesis is a statement that will be accepted only if there is convincing sample evidence that it is true.

The exact shape of the chi-square distribution depends on the degrees of freedom.

After testing H₀: p = .33;versus H_A: p< .33;at α = .05,with 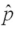= .20 and n = 100,we do not reject H₀.

A recent study conducted by the state government attempts to determine whether the voting public supports a further increase in cigarette taxes.The opinion poll recently sampled 1500 voting age citizens.1020 of the sampled citizens were in favor of an increase in cigarette taxes.The state government would like to decide if there is enough evidence to establish whether the proportion of citizens supporting an increase in cigarette taxes is significantly greater than .66.Identify the null hypothesis.

A cereal manufacturer is concerned that the boxes of cereal not be underfilled or overfilled.Each box of cereal is supposed to contain 13 ounces of cereal.A random sample of 31 boxes is tested.The average weight is 12.58 ounces,and the standard deviation is 0.25 ounces.Calculate a confidence interval to test the hypotheses at α = .10.

Based on a random sample of 25 units of product X,the average weight is 102 lbs.and the sample standard deviation is 10 lbs.We would like to decide if there is enough evidence to establish that the average weight for the population of product X is greater than 100 lbs.Assume the population is normally distributed.What is the critical value used to test the claim at α = .05?

For a given hypothesis test,if we do not reject H₀,and H₀ is true,

Everything else being constant,increasing the sample size decreases the probability of committing a Type II error.

A cereal manufacturer is concerned that the boxes of cereal not be underfilled or overfilled.Each box of cereal is supposed to contain 13 ounces of cereal.A random sample of 31 boxes is tested.The average weight is 12.58 ounces,and the standard deviation is 0.25 ounces.Calculate the test statistic to test the hypotheses.

When conducting a hypothesis test about a single mean,reducing the level of significance (α)will increase the size of the rejection region.

It is estimated that the average person in the United States uses 123 gallons of water per day.Some environmentalists believe this figure is too high and conduct a survey of 40 randomly selected Americans.They find a mean of 113.03 gallons and a population standard deviation of 25.99 gallons.Calculate the p-value for this test statistic,and test the hypothesis at α = .01.

The HR department tested how long employees stay with the company in their current positions.A random sample of 50 employees yielded a mean of 2.79 years and σ = .76.The sample evidence indicates that the average time is less than 3 years and is significant at α = .01.

In testing H₀: μ ≤ 23;versus H_A: μ > 23,when 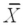= 26,σ = 6,and n = 30,what is the value of the test statistic?