Exam 9: Hypothesis Testing

You cannot make a Type II error when the null hypothesis is true.

For a hypothesis test about a population proportion or mean,if the level of significance is less than the p-value,the null hypothesis is rejected.

The manager of the quality department for a tire manufacturing company wants to know the average tensile strength of rubber used in making a certain brand of radial tire.The population is normally distributed and the population standard deviation is known.She uses a z test to test the null hypothesis that the mean tensile strength is 800 pounds per square inch.The calculated z test statistic is a positive value that leads to a p-value of .045 for the test.If the significance level (α)is .05,the null hypothesis would be rejected.

If a null hypothesis is rejected at a significance level of .05,it will _____________ be rejected at a significance level of .01.

It has been hypothesized that on average employees spend one hour a day playing video games at work.To test this at her company,a manager takes a random sample of 35 employees,who showed a mean time of 55 minutes per day with an assumed population standard deviation of 5 minutes.What is the critical value for testing these hypotheses at α = .01?

A Type II error is defined as the probability of ________________ H₀,when it should _____________.

Based on a random sample of 25 units of product X,the average weight is 102 lbs.and the sample standard deviation is 10 lbs.We would like to decide if there is enough evidence to establish that the average weight for the population of product X is greater than 100 lbs.Assume the population is normally distributed.What is the critical value to test the claim at α = .01?

Based on a random sample of 25 units of product X,the average weight is 102 lbs.and the sample standard deviation is 10 lbs.We would like to decide if there is enough evidence to establish that the average weight for the population of product X is greater than 100 lbs.Assume the population is normally distributed.What is the p-value for this test?

We are testing H₀: μ ≤ 8;versus H_A: μ > 8.Given α = .01,n = 25, 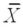= 8.112,and s = .16,we should reject the H₀.(Assume the sample is selected from a normally distributed population. )

A manufacturer of an automobile part has a process that is designed to produce the part with a target of 2.5 inches in length.In the past,the standard deviation of the length has been 0.035 inches.In an effort to reduce the variation in the process,the manufacturer has redesigned the process.A sample of 25 parts produced under the new process shows a sample standard deviation of 0.025 inches.Test the claim that the new process standard deviation has improved from the current process at α = .05.

Using a χ² test statistic to test the null hypothesis that the variance of a new process is equal to the variance of the current process and rejecting at a p-value less than α,we can conclude that the new process is more consistent than the current process.

When evaluating a new process,using the square root of the upper end of the confidence interval for σ² gives an estimate of the smallest that σ for the new process might reasonably be.

When computing a 95 percent confidence interval for σ² with a sample of n = 30,we would use the following values of χ² in the calculations:

A survey of the wine market has shown that the preferred wine for 17 percent of Americans is merlot.A wine producer in California,where merlot is produced,believes the figure is higher in California.She contacts a random sample of 550 California residents and asks which wine they purchase most often.Suppose 115 replied that merlot was the primary wine.Calculate the p-value associated with the test statistic,and test the claim at α = .01.

A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line.The machine that dispenses dressing is working properly when 8 ounces are dispensed.The standard deviation of the process is 0.15 ounces.A sample of 48 bottles is selected periodically,and the filling line is stopped if there is evidence that the mean amount dispensed is different from 8 ounces.Suppose that the mean amount dispensed in a particular sample of 48 bottles is 7.983 ounces.Calculate the test statistic.

To compute a 95 percent confidence interval for σ²,we use n - 1 degrees of freedom and the chi-square points on the distribution curve of χ_α/2² and of χ_1-(α/2)².

If you live in California,the decision to buy earthquake insurance is an important one.A survey revealed that only 133 of 337 randomly selected residences in one California county were protected by earthquake insurance.Calculate the appropriate test statistic to test the claim that less than 40 percent of the residents in the county are protected by earthquake insurance.

A recent study conducted by the state government attempts to determine whether the voting public supports a further increase in cigarette taxes.The opinion poll recently sampled 1500 voting age citizens.1020 of the sampled citizens were in favor of an increase in cigarette taxes.The state government would like to decide if there is enough evidence to establish whether the proportion of citizens supporting an increase in cigarette taxes is significantly greater than .66.The alternative hypothesis is:

For the following hypothesis test,where H₀: μ ≤ 10;vs.H_A: μ > 10,we reject H₀ at level of significance α and conclude that the true mean is greater than 10,when the true mean is really 14.Based on this information,we can state that we have:

A recent study conducted by the state government attempts to determine whether the voting public supports a further increase in cigarette taxes.The opinion poll recently sampled 1500 voting age citizens.1020 of the sampled citizens were in favor of an increase in cigarette taxes.The state government would like to decide if there is enough evidence to establish whether the proportion of citizens supporting an increase in cigarette taxes is significantly greater than .66.At α = .10,we would not reject H₀.