Exam 5: Inequalities and Linear Programming
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
Solve the following linear programming problem.
Minimize 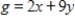 subject to
subject to
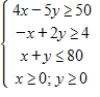
(Multiple Choice)
4.9/5  (34)
(34)
The final simple matrix for a minimization problem is given below. Find the solution. 
(Multiple Choice)
4.9/5  (36)
(36)
Nolan Industries manufactures water filters/purifiers that attach to a kitchen faucet. Each purifier consists of a housing unit that attaches to the faucet and a 60-day filter that is inserted into the housing. Past records indicate that on average the number of filters produced plus the number of housing units produced should be at least 500 per week. It takes 20 minutes to make and assemble each filter and 40 minutes for each housing. The manufacturing facility has up to 20,000 minutes per week for making and assembling these units, but due to certain parts' supply constraints, the number of housing units per week can be at most 400. If manufacturing costs (for material and labor) are $7.25 for each filter and $8.55 for each housing unit, how many of each should be produced to minimize weekly costs? Find the minimum cost.
(Multiple Choice)
4.9/5  (35)
(35)
A cereal manufacturer makes two different kinds of cereal, Senior Citizen's Feast and Kids Go. Each pound of Senior Citizen's Feast requires 0.6 lb of wheat and 0.2 lb of vitamin-enriched syrup, and each pound of Kids Go requires 0.4 lb of wheat, 0.2 lb of sugar, and 0.2 lb of vitamin-enriched syrup. Suppliers can deliver at most 2,800 lb of wheat, at most 800 lb of sugar, and at least 1,000 lb of the vitamin-enriched syrup. If the profit is $0.80 on each pound of Senior Citizen's Feast and $1.00 on each pound of Kids Go, find the number of pounds of each cereal that should be produced to obtain maximum profit. Find the maximum profit. Round your profit to the nearest cent, another answers - to the nearest whole number.
(Multiple Choice)
4.9/5  (43)
(43)
Use the simplex method to maximize the given function. Assume all variables are nonnegative.
Maximize 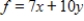 subject to
subject to
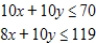
(Multiple Choice)
4.8/5  (35)
(35)
A simplex matrix for a standard maximization problem is given. Indicate whether or not the solution shown is complete (optimal). If the solution is not complete, find the next pivot or indicate that no solution exists. 
(Multiple Choice)
4.8/5  (31)
(31)
A simplex matrix for a standard maximization problem is given. Indicate whether or not the solution shown is complete (optimal). If the solution is not complete, find the next pivot or indicate that no solution exists. 
(Multiple Choice)
4.8/5  (33)
(33)
An experiment that involves learning in animals requires placing white mice and rabbits into separate, controlled environments, environment I and environment II. The maximum amount of time available in environment I is 200 minutes, and the maximum amount of time available in environment II is 100 minutes. The white mice must spend 16 minutes in environment I and 20 minutes in environment II, and the rabbits must spend 15 minutes in environment I and 50 minutes in environment II. Write a system of inequalities that describes the constraints on the number of each type of animal used in the experiment. Let x denote the number of white mice and y denote the number of rabbits.
(Multiple Choice)
4.7/5  (27)
(27)
Patio Iron makes wrought iron outdoor dining tables, chairs, and stools. Each table uses 8 ft of a standard-width wrought iron, 2 hours of labor for cutting and assembly, and 2 hours of labor for detail and finishing work. Each chair uses 6 ft of the wrought iron, 2 hours of cutting and assembly labor, and 1.5 hours of detail and finishing labor. Each stool uses 1 ft of the wrought iron, 1.5 hours for cutting and assembly, and 0.5 hour for detail and finishing work, and the daily demand for stools is at most 16. Each day Patio Iron has available at most 108 ft of wrought iron, 50 hours for cutting and assembly, and 40 hours for detail and finishing. If the profits are $60 for each dining table, $49 for each chair, and $39 for each stool, how many of each item should be made each day to maximize profit? Find the maximum profit. Round your profit to the nearest dollar and another answers - to the nearest whole number.
(Multiple Choice)
4.8/5  (34)
(34)
A sausage company makes two different kinds of hot dogs, regular and beef. Each pound of beef hot dogs requires 0.75 lb of beef and 0.2 lb of spices, and each pound of regular hot dogs requires 0.17 lb of beef, 0.31 lb of pork, and 0.22 lb of spices. Suppliers can deliver at most 1020 lb of beef, at most 600 lb of pork, and at least 500 lb of spices. Let x represent the number of pounds of regular meat and y represent the number of pounds of beef. Write the inequalities that describe how many pounds of each type of hot dog can be produced.
(Multiple Choice)
4.8/5  (25)
(25)
Use the simplex method, Excel, or another technology, to find the solution of the problem given below. Assume all variables are nonnegative. 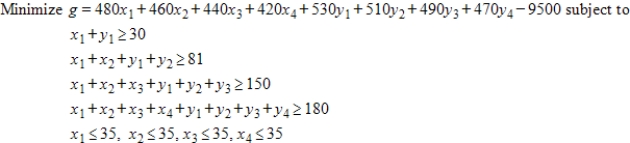
(Multiple Choice)
4.9/5  (34)
(34)
Find the transpose of the matrix associated with the given minimization problem. y Minimize 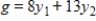 subject to
subject to
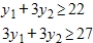
(Multiple Choice)
4.9/5  (37)
(37)
Two foods contain only proteins, carbohydrates, and fats. Food A costs $1.30 per pound and contains 30% protein and 50% carbohydrates. Food B costs $1.95 per pound and contains 20% protein and 75% carbohydrates. What combination of these two foods provides at least 1 pound of protein, 2.5 pounds of carbohydrates, and 0.25 pounds of fat at the lowest cost? Round your answer to the nearest cent.
(Multiple Choice)
4.9/5  (37)
(37)
Write the dual maximization problem. Be sure to rename the variables.
Minimize 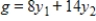 subject to
subject to
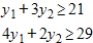
(Multiple Choice)
4.8/5  (32)
(32)
A manufacturer makes Portable Satellite Radios and Auto Satellite Radios at plants in Lakeland and Rockledge. At the Lakeland plant, at most 1800 radios can be produced, and the production of the Auto Satellite Radios can be at most 200 fewer than the production of the Portable Satellite Radios. At the Rockledge plant, at most 1200 radios can be produced. The profits on the Portable Satellite Radios are $101 at Lakeland and $93 at Rockledge, and the profits on the Auto Satellite Radios are $71 at Lakeland and $76 at Rockledge. If the manufacturer gets a rush order for 1500 Portable Satellite Radios and 1300 Auto Satellite Radios, how many of each should be produced at each location so as to maximize profits? Find the maximum profit.
(Multiple Choice)
4.9/5  (40)
(40)
The Wellbuilt Company produces two types of wood chippers, economy and deluxe. The deluxe model requires 3 hours to assemble and 0.5 hour to paint, and the economy model requires 2 hours to assemble and 1 hour to paint. The maximum number of assembly hours available is 24 per day, and the maximum number of painting hours available is 8 per day. If the profit on the deluxe model is $18 per unit and the profit on the economy model is $14 per unit, find the maximum profit. Round your answer to the nearest dollar if necessary.
(Multiple Choice)
4.8/5  (35)
(35)
Showing 21 - 40 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)