Exam 5: Inequalities and Linear Programming
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
At one of its factories, a jeans manufacturer makes two styles: #891 and #917. Each pair of style-891 takes 10 minutes to cut out and 20 minutes to assemble and finish. Each pair of style-917 takes 10 minutes to cut out and 30 minutes to assemble and finish. The plant has enough workers to provide at most 7,500 minutes per day for cutting and at most 19,500 minutes per day for assembly and finishing. The profit on each pair of style-891 is $6.00 and the profit on each pair of style-917 is $8.50. How many pairs of each style should be produced per day to obtain maximum profit? Find the maximum daily profit. Round your profit to the nearest cent and anothet answers - to the nearest whole number.
(Multiple Choice)
4.7/5  (42)
(42)
Form the simplex matrix, and identify the first pivot entry. Minimize 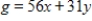 subject to
subject to 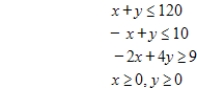
(Multiple Choice)
4.9/5  (36)
(36)
A contractor builds two types of homes. The Carolina requires one lot, $160,000 capital, and 160 worker-days of labor, whereas the Savannah requires one lot, $240,000 capital, and 160 worker-days of labor. The contractor owns 300 lots and has $48,000,000 available capital and 43,200 worker-days of labor. The profit on the Carolina is $40,000 and the profit on the Savannah is $52,000. Use the corner points of the feasible region to find how many of each type of home should be built to maximize profit. Find the maximum possible profit. Round your profit to the nearest dollar, another answers - to the nearest whole number.
(Multiple Choice)
4.7/5  (28)
(28)
Suppose that three water purification facilities can handle at most 22 million gallons in a certain time period. Plant 1 leaves 20% of certain impurities, and costs $20,000 per million gallons. Plant 2 leaves 15% of these impurities and costs $30,000 per million gallons. Plant 3 leaves 10% impurities and costs $40,000 per million gallons. The desired level of impurities in the water from all three plants is at most 15%. If Plant 1 and Plant 3 combined must handle at least 18 million gallons, find the number of gallons each plant should handle so as to achieve the desired level of purity at minimum cost. Find the minimum cost.
(Multiple Choice)
4.8/5  (39)
(39)
A company manufactures commercial heating system components and domestic furnaces at its factories in Monaca, PA and Hamburg, NY. At the Monaca plant, no more than 1000 units per day can be produced, and the number of commercial components cannot exceed 100 more than half the number of domestic furnaces. At the Hamburg plant, no more than 850 units per day can be produced. The profit on each commercial component is $400 at the Monaca plant and $390 at the Hamburg plant. The profit on each domestic furnace is $200 at the Monaca plant and $215 at the Hamburg plant. If there is a rush order for 540 commercial components and 740 domestic furnaces, how many of each should be produced at each plant in order to maximize profits? Find the maximum profit. Note: Assume that exactly enough units are produced to fill the rush order.
(Multiple Choice)
4.8/5  (37)
(37)
Use the given feasible region determined by the constraint inequalities to find the maximum and minimum of the given objective function (if they exist). 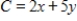
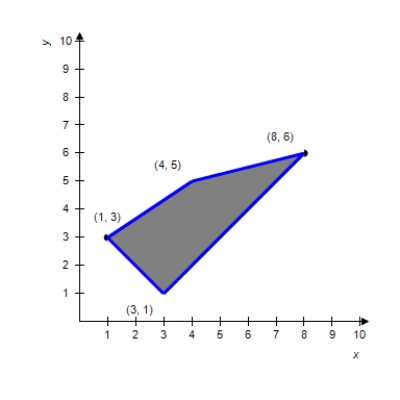
(Multiple Choice)
5.0/5  (43)
(43)
Use the simplex method to find the optimal solution.
Maximize 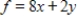 subject to
subject to 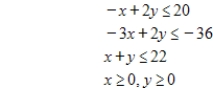
(Multiple Choice)
4.8/5  (39)
(39)
A medical clinic performs three types of medical tests that use the same machines. Tests A, B, and C take 15 minutes, 30 minutes, and 1 hour, respectively, with respective profits of $40, $80 and $110. The clinic has 4 machines available. One person is qualified to do test A, two to do test B, and one to do test C. If the clinic has a rush of customers for these tests, how many of each type should it schedule in a 12 - hour day to maximize its profit? Round your profit to the nearest dollar and another answers - to the nearest whole number.
(Multiple Choice)
4.8/5  (38)
(38)
A car rental agency has a budget of $1.8 million to purchase at most 100 new cars. The agency will purchase either compact cars at $15,000 each or luxury cars at $30,000 each. From past rental patterns, the agency decides to purchase at most 50 luxury cars and expects an annual profit of $8,000 per compact car and $13,500 per luxury car. How many of each type of car should be purchased in order to obtain the maximum profit while satisfying budgetary and other planning constraints? Find the maximum profit. Round your profit to the nearest dollar and another answers - to the nearest whole number.
(Multiple Choice)
4.7/5  (31)
(31)
Write the dual maximization problem. Be sure to rename the variables.
Minimize 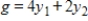 subject to
subject to
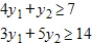
(Multiple Choice)
4.7/5  (34)
(34)
The graph of the feasible region is shown. Locate the corners of the feasible region in order to find the minimum of the given objective function (if it exists). 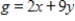
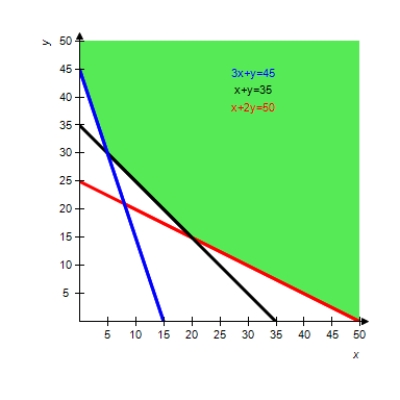
(Multiple Choice)
4.8/5  (34)
(34)
A farm co-op has 6,000 acres available to plant with corn and soybeans. Each acre of corn requires 9 gallons of fertilizer/herbicide and 0.75 hour of labor to harvest. Each acre of soybeans requires 3 gallons of fertilizer/herbicide and 1hour of labor to harvest. The co-op has available at most 40,508 gallons of fertilizer/herbicide and at most 5,250 hours of labor for harvesting. Find the maximum profit if the profits per acre are $65 for corn and $50 for soybeans. Round your answer to the nearest cent if necessary.
(Multiple Choice)
4.8/5  (24)
(24)
Form the matrix associated with the given minimization problem and find its transpose.
Minimize 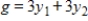 subject to
subject to
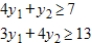
(Multiple Choice)
4.9/5  (38)
(38)
Write the dual maximization problem.
Minimize 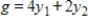 subject to
subject to
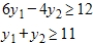
(Multiple Choice)
4.9/5  (32)
(32)
A company manufactures two types of electric hedge trimmers, one of which is cordless. The cord-type trimmer requires 6 hours to make, and the cordless model requires 1.5 hours. The company has only 800 work hours to use in manufacturing each day, and the packaging department can package only 300 trimmers per day. Let x represent the number of cord type models and y represent the number of cordless models. Graph the solution of the system of inequalities.
(Multiple Choice)
4.8/5  (42)
(42)
Apex Motors manufactures luxury cars and sport utility vehicles. The most likely customers are high-income men and women, and company managers want to initiate an advertising campaign targeting these groups. They plan to run 1-minute spots on business/investment programs, where they can reach 7 million women and 4 million men from their target groups. They also plan 1-minute spots during sporting events, where they can reach 2 million women and 12 million men from their target groups. Apex feels that the ads must reach at least 40 million women and at least 24 million men who are prospective customers. Let x represent the number of minutes of business/investment program commercials and y represent the number of minutes of sporting events commercials. Write the inequalities that describe the constraints on the number of each type of 1-minute spots needed to reach these target groups.
(Multiple Choice)
4.8/5  (36)
(36)
Solve the following linear programming problem.
Maximize 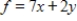 subject to
subject to
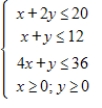
(Multiple Choice)
4.8/5  (29)
(29)
Solve the following minimization problem by solving the primal problem with the simplex method.
Minimize 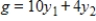 subject to
subject to
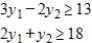
(Multiple Choice)
4.7/5  (36)
(36)
A cereal manufacturer makes two different kinds of cereal, Senior Citizen's Feast and Kids Go. Each pound of Senior Citizen's Feast requires 0.7 lb of wheat and 0.2 lb of vitamin-enriched syrup, and each pound of Kids Go requires 0.4 lb of wheat, 0.2 lb of sugar, and 0.2 lb of vitamin-enriched syrup. Suppliers can deliver at most 2800 lb of wheat, at most 800 lb of sugar, and at least 1000 lb of the vitamin-enriched syrup. Let x represent the number of pounds of Senior Citizen's cereal and y represent the number of pounds of Kids Go cereal. Write the inequalities that describe how many pounds of each type of cereal can be made.
(Multiple Choice)
4.9/5  (46)
(46)
Showing 101 - 120 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)