Exam 5: Inequalities and Linear Programming
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
Solve both the primal and dual problems with the simplex method. Use f to represent the dual objective function. Minimize 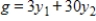 subject to
subject to 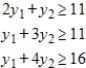
(Multiple Choice)
4.8/5  (37)
(37)
Solve the following linear programming problem.
Maximize 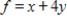 subject to
subject to
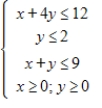
(Multiple Choice)
4.9/5  (31)
(31)
Use the simplex method to maximize the function (if possible) subject to the given constraints. If there is no solution, indicate this; if multiple solutions exist, give one solution.
Maximize 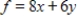 subject to
subject to
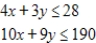
(Multiple Choice)
4.9/5  (35)
(35)
A political candidate wishes to use a combination of radio and TV advertisements in her campaign. Research has been shown that each 1-minute spot on TV reaches 0.6 million people and that each 1 -minute spot on radio reaches 0.4 million. The candidate feels she must reach 42 million people, and she must buy at least 54 minutes of advertisements. How many minutes of each medium should be used if TV costs $550 per minute, radio costs $110 per minute, and the candidate wishes to minimize costs?
(Multiple Choice)
5.0/5  (37)
(37)
Form the simplex matrix for the problem given below. Maximize 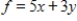 subject to
subject to 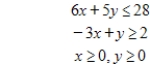
(Multiple Choice)
4.9/5  (40)
(40)
A candidate wishes to use a combination of radio and television advertisements in her campaign. Assume that each 1-minute spot on television reaches to 0.0765 million people and that each 1-minute spot on radio reaches to 0.0045 million. The candidate feels she must reach at least 7.425 million people, and she must buy total of at least 90 minutes of advertisements. How many minutes of each medium should be used to minimize costs if television costs $450 per minute and radio costs $75 per minute? Round your answer to nearest integer if necessary.
(Multiple Choice)
4.9/5  (29)
(29)
Use Excel or another technology to solve the following optimization problem. Minimize 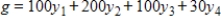 subject to
subject to 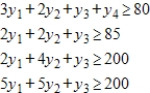
(Multiple Choice)
4.8/5  (29)
(29)
The graph of the feasible region is shown. Locate the corners of the feasible region in order to find the maximum of the given objective function (if it exists). 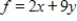
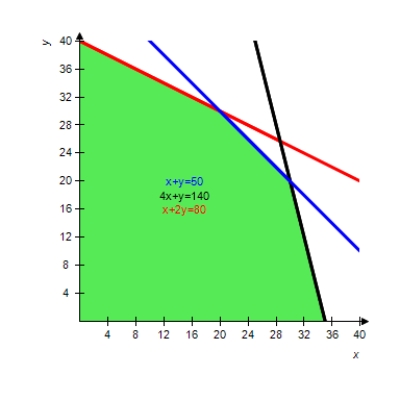
(Multiple Choice)
4.9/5  (34)
(34)
Three factories each dump waste water containing three different types of pollutants into a river. State regulations require the factories to treat their waste in order to reduce pollution levels. The table shows the possible percent reduction of each pollutant at each site and the cost per ton to process the waste. 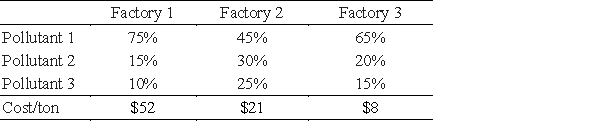
If the state requires a reduction of at least 65 tons per day of pollutant 1, at least 40 tons per day of pollutant 2, and at least 20 tons per day of pollutant 3, find the number of tons of waste that must be treated each day at each site so that the state's requirements are satisfied and the treatment costs are minimized. Find the minimum cost.
If the state requires a reduction of at least 65 tons per day of pollutant 1, at least 40 tons per day of pollutant 2, and at least 20 tons per day of pollutant 3, find the number of tons of waste that must be treated each day at each site so that the state's requirements are satisfied and the treatment costs are minimized. Find the minimum cost.
(Multiple Choice)
4.9/5  (39)
(39)
CDF Appliances has assembly plants in Atlanta and Fort Worth where they produce a variety of kitchen appliances, including a 12-cup coffee maker and a cappuccino machine. In each hour at the Atlanta plant, 160 of the 12-cup models and 200 of the cappuccino machines can be assembled and the hourly cost is $780. In each hour at the Fort Worth plant, 800 of the 12-cup models and 200 of the cappuccino machines can be assembled and the hourly cost is $2,120. CDF Appliances expects orders each week for at least 64,000 of the 12-cup models and at least 40,000 of the cappuccino machines. How many hours per week should each plant be operated in order to provide inventory for the orders at minimum cost? Find the minimum cost.
(Multiple Choice)
4.9/5  (39)
(39)
A farm co-op has 6,000 acres available to plant with corn and soybeans. Each acre of corn requires 9 gallons of fertilizer/herbicide and 0.75 hour of labor to harvest. Each acre of soybeans requires 3 gallons of fertilizer/herbicide and 1hour of labor to harvest. The co-op has available at most 40,501 gallons of fertilizer/herbicide and at most 5,250 hours of labor for harvesting. Find the maximum profit if the profits per acre are $75 for corn and $40 for soybeans. Round your answer to the nearest cent if necessary.
(Multiple Choice)
4.9/5  (41)
(41)
A primal maximization problem is given. Solve both the primal and dual problems with the simplex method.
Maximize 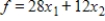 subject to
subject to
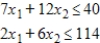
(Multiple Choice)
4.8/5  (39)
(39)
Use the simplex method to find the optimal solution.
Maximize 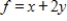 subject to
subject to 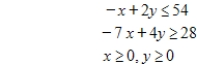
(Multiple Choice)
4.9/5  (37)
(37)
Use the simplex method to maximize the given function. Assume all variables are nonnegative.
Maximize 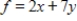 subject to
subject to
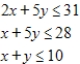
(Multiple Choice)
4.7/5  (41)
(41)
State the following problem in a form for which the simplex matrix can be formed (that is, as a maximization problem with  constraints).
constraints). 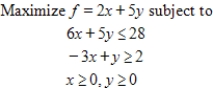
(Multiple Choice)
4.7/5  (35)
(35)
Use the simplex method to find the optimal solution. Minimize 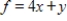 subject to
subject to 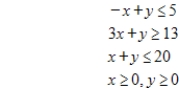
(Multiple Choice)
4.7/5  (29)
(29)
Suppose that in a hospital ward, the patients can be grouped into two general categories depending on their condition and the amount of solid foods they require in their diet. A combination of two diets is used for solid foods because they supply essential nutrients for recovery. The table below summarizes the patient groups and their minimum daily requirements. Let x represent number of servings of Diet A and y represent number of servings of Diet B. Write the inequalities that describe how many servings of each diet are needed to provide the nutritional requirements. 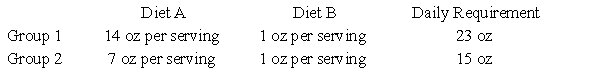
(Multiple Choice)
4.9/5  (26)
(26)
A sausage company makes two different kinds of hot dogs, regular and all beef. Each pound of all-beef hot dogs requires 0.75 lb of beef and 0.2 lb of spices, and each pound of regular hot dogs requires 0.18 lb of beef, 0.3 lb of pork, and 0.2 lb of spices. Suppliers can deliver at most 1,020 lb of beef, at most 600 lb of pork, and at least 500 lb of spices. If the profit is $0.70 on each pound of all-beef hot dogs and $0.40 on each pound of regular hot dogs, how many pounds of each should be produced to obtain maximum profit? What is the maximum profit? Round your profit to the nearest cent, another answers - to the nearest whole number.
(Multiple Choice)
5.0/5  (44)
(44)
A chemical storage tank has a capacity of 200 tons. Currently, the tank contains 50 tons of a mixture that has 10% of a certain active chemical and 1.8% of other inert ingredients. The owners of the tank want to replenish the supply in the tank and will purchase some combination of two available mixes. Mix 1 contains 70% of the active chemical and 3% of the inert ingredients; its cost is $107 per ton. Mix 2 contains 30% of the active chemical and 1% of the inert ingredients; its cost is $46 per ton. The desired final mixture should have at least 40% of the active chemical and at most 2% of the inert ingredients. How many tons of each mix should be purchased to obtain the desired final mixture at minimum cost? Find the minimum cost. Note that at least 40% of the active chemical means 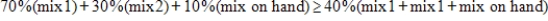
(Multiple Choice)
4.9/5  (24)
(24)
Showing 81 - 100 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)