Exam 5: Inequalities and Linear Programming
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
Use the simplex method to maximize the function (if possible) subject to the given constraints. If there is no solution, indicate this; if multiple solutions exist, give one solution.
Maximize 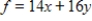 subject to
subject to
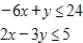
(Multiple Choice)
4.8/5  (34)
(34)
Suppose a ball manufacturer produces soccer balls, footballs, and volleyballs. The manager feels that restricting the types of balls produced could increase revenue. The following table gives the price of each ball, the raw materials cost, and the profit on each ball. The monthly profit must be at least $40,000, and the raw materials costs must be no more than $50,000. How many of each type of ball should be produced to maximize the revenue? What is the maximum revenue? 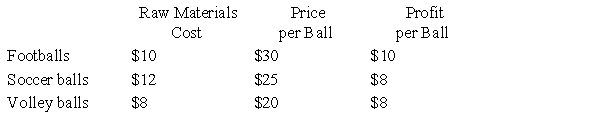
(Multiple Choice)
4.9/5  (39)
(39)
Use the simplex method, Excel, or another technology to find the solution of the problem given below. Assume all variables are nonnegative. Maximize 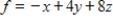
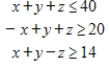
(Multiple Choice)
4.7/5  (38)
(38)
At one of its factories, a jeans manufacturer makes two styles: #891 and #917. Each pair of style-891 takes 10 minutes to cut out and 20 minutes to assemble and finish. Each pair of style-917 takes 10 minutes to cut out and 30 minutes to assemble and finish. The plant has enough workers to provide at most 7,500 minutes per day for cutting and at most 19,500 minutes per day for assembly and finishing. The profit on each pair of style-891 is $6.00 and the profit on each pair of style-917 is $9.50. Find the maximum daily profit. Round your answer to the nearest cent if necessary.
(Multiple Choice)
4.7/5  (39)
(39)
A cereal manufacturer makes two different kinds of cereal, Senior Citizen's Feast and Kids Go. Each pound of Senior Citizen's Feast requires 0.8 lb of wheat and 0.2 lb of vitamin-enriched syrup, and each pound of Kids Go requires 0.4 lb of wheat, 0.2 lb of sugar, and 0.2 lb of vitamin-enriched syrup. Suppliers can deliver at most 2880 lb of wheat, at most 850 lb of sugar, and at least 900 lb of the vitamin-enriched syrup. Let x represent the number of pounds of Senior Citizen's cereal and y represent the number of pounds of Kids Go cereal. Graph the region determined by the constraint inequalities.
(Multiple Choice)
4.7/5  (31)
(31)
Suppose a primal minimization problem and its dual maximization problem were solved by using the simplex method on the dual problem. The final simplex matrix is given. Find the solution of the minimization problem. Use y1, y2, y3 as the variables and g as the function. 
(Multiple Choice)
4.8/5  (25)
(25)
A primal maximization problem is given. Form the dual minimization problem.
Maximize 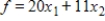 subject to
subject to
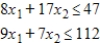
(Multiple Choice)
4.8/5  (36)
(36)
A farm co-op has over 40,500 gallons of fertilizer/herbicide available to use when planting corn and soybeans. The farm co-op's maximum profit for using 40,500 gallons of fertilizer/herbicide is $315,002 and the maximum profit for 40,508 gallons is $315,030. What is the profit value of each additional gallon of fertilizer/herbicide (that is, the shadow price of a gallon of fertilizer/herbicide)? Round your answer to the nearest cent if necessary.
(Multiple Choice)
4.8/5  (36)
(36)
A simplex matrix is given. In this case, the solution is complete, so identify the maximum value of f and a set of values for the variables that gives this maximum value. If multiple solutions may exist, indicate this and locate the next pivot. 
(Multiple Choice)
4.9/5  (32)
(32)
Suppose that in a hospital ward, the patients can be grouped into two general categories depending on their condition and the amount of solid foods they require in their diet. A combination of two diets is used for solid foods because they supply essential nutrients for recovery. The table below summarizes the patient groups and their minimum daily requirements. Let x represent the number of servings of A and y represent the number of servings of B. Determine the inequalities that describe how many servings of each diet are needed to provide the nutritional requirements and then graph the region determined by these constraint inequalities. 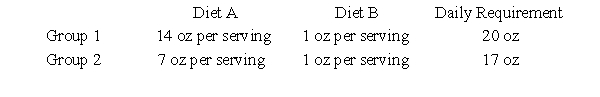
(Multiple Choice)
4.8/5  (28)
(28)
Tire Corral has $6,000 available per month for advertising. Newspaper ads cost $100 each and can occur a maximum of 21 times per month. Radio ads cost $300 each and can occur a maximum of 28 times per month at this price. Each newspaper ad reaches 6,750 men over 20 years of age, and each radio ad reaches 8,500 of these men. The company wants to maximize the number of ad exposures to this group. How many of each ad should it purchase? What is the maximum possible number of exposures? Round your answers to the nearest whole number if necessary.
(Multiple Choice)
4.9/5  (35)
(35)
Apex Motors manufactures luxury cars and sport utility vehicles. The most likely customers are high-income men and women, and company managers want to initiate an advertising campaign targeting these groups. They plan to run 1-minute spots on business/investment programs, where they can reach 7 million women and 4 million men from their target groups. They also plan 1-minute spots during sporting events, where they can reach 2 million women and 12 million men from their target groups. Apex feels that the ads must reach at least 32 million women and at least 20 million men who are prospective customers. Let x represent the number of minutes of business/investment program commercials and y represent the number of minutes of sporting events commercials. Graph the region determined by the constraint inequalities.
(Multiple Choice)
4.8/5  (31)
(31)
Use the simplex method, Excel, or another technology to solve.
Maximize 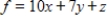 subject to
subject to 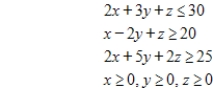
(Multiple Choice)
4.9/5  (35)
(35)
Use the simplex method to find the optimal solution.
Minimize 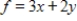 subject to
subject to 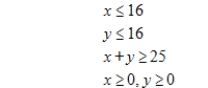
(Multiple Choice)
4.7/5  (41)
(41)
Solve the following linear programming problem. Minimize 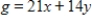 subject to
subject to
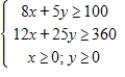
(Multiple Choice)
4.9/5  (36)
(36)
Use the simplex method to maximize the given function. Assume all variables are nonnegative.
Maximize 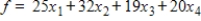 subject to
subject to
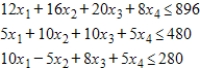
(Multiple Choice)
4.7/5  (33)
(33)
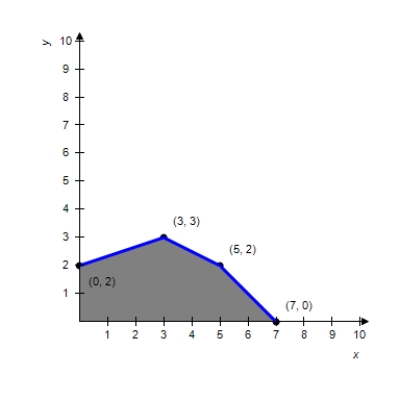
Use the given feasible region determined by the constraint inequalities to find the maximum and minimum of the objective function 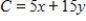 .
. 
(Multiple Choice)
4.8/5  (37)
(37)
Showing 41 - 60 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)