Exam 6: Exponential and Logarithmic Functions
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
If $6,000 is invested at an annual rate of 9% per year compounded monthly, the future value S at any time t (in months) is given by 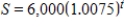 . What is the amount after 1 year? Round your answer to the nearest cent.
. What is the amount after 1 year? Round your answer to the nearest cent.
(Multiple Choice)
4.9/5  (44)
(44)
Use the formula 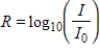 . In October 2004, an earthquake measuring 6.8 on the Richter scale occurred in Japan. The largest quake in Japan since 1990was one in 1993that registered 7.7. How many times more severe was the 1993shock than the one in 2004on the Richter scale? Round your answer to one decimal place.
. In October 2004, an earthquake measuring 6.8 on the Richter scale occurred in Japan. The largest quake in Japan since 1990was one in 1993that registered 7.7. How many times more severe was the 1993shock than the one in 2004on the Richter scale? Round your answer to one decimal place.
(Multiple Choice)
4.9/5  (40)
(40)
If $9,000 is invested at an annual rate of 11% per year compounded monthly, the future value S at any time t (in months) is given by 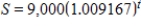 . How long does it take for the investment to double? Round your answer to one decimal place.
. How long does it take for the investment to double? Round your answer to one decimal place.
(Multiple Choice)
4.9/5  (40)
(40)
Solve the exponential equation. Give answers correct to 3 decimal places. 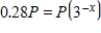
(Multiple Choice)
4.7/5  (39)
(39)
The consumer price index (CPI) is calculated by averaging the prices of various items after assigning a weight to each item. The following table gives the consumer price indexes for selected years from 1940 through 2002, reflecting buying patterns of all urban consumers, with x representing years past 1900. Find an equation that models these data. If it's necessary, round your calculations to four decimal places. 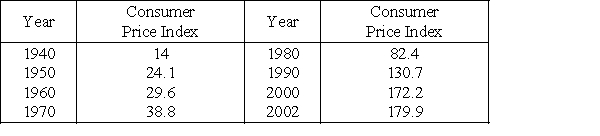
Source: U.S. Bureau of the Census
Source: U.S. Bureau of the Census
(Multiple Choice)
4.7/5  (25)
(25)
Use properties of logarithms or a definition to simplify the expression. Check the result with a change-of-base formula and a calculator. 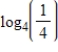
(Multiple Choice)
4.7/5  (40)
(40)
If the supply function for a product is given by 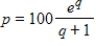 , where q represents the number of hundreds of units, what will be the price when the producers are willing to supply 500 units? Round your answer to the nearest cent.
, where q represents the number of hundreds of units, what will be the price when the producers are willing to supply 500 units? Round your answer to the nearest cent.
(Multiple Choice)
4.8/5  (41)
(41)
The monthly sales S for a product is given by 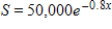 , where x is the number of months that have passed since the end of a promotional campaign. Determine the monthly sales 4 months after the promotional campaign. Round your answer to the nearest cent.
, where x is the number of months that have passed since the end of a promotional campaign. Determine the monthly sales 4 months after the promotional campaign. Round your answer to the nearest cent.
(Multiple Choice)
4.9/5  (31)
(31)
For selected years from 1978 to 2002, the number of mutual funds N, excluding money market funds, can be modeled by 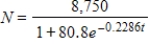 , where t is the number of years past 1975 (Source: Investment Company Institute, Mutual Fund Fact Book (2003)). Use the model to estimate the year when the number of mutual funds will reach 8,000.
, where t is the number of years past 1975 (Source: Investment Company Institute, Mutual Fund Fact Book (2003)). Use the model to estimate the year when the number of mutual funds will reach 8,000.
(Multiple Choice)
4.9/5  (25)
(25)
By using data from the U.S. Bureau of Labor Statistics for the years 1968-2002, the purchasing power P of a 1983 dollar can be modeled with the function 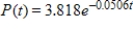 , where t is the number of years past 1960. In what year will the purchasing power of a 1983 dollar be $0.10? Round-up your answer to the nearest year.
, where t is the number of years past 1960. In what year will the purchasing power of a 1983 dollar be $0.10? Round-up your answer to the nearest year.
(Multiple Choice)
4.8/5  (34)
(34)
By using data from the U.S. Bureau of Labor Statistics for the years 1968-2002, the purchasing power P of a 1983 dollar can be modeled with the function 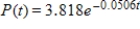 , where t is the number of years past 1960. Based on this model, what is the purchasing power of a 1983 dollar in the year 1970? Round your answer to the nearest cent.
, where t is the number of years past 1960. Based on this model, what is the purchasing power of a 1983 dollar in the year 1970? Round your answer to the nearest cent.
(Multiple Choice)
4.8/5  (30)
(30)
Use a change-of-base formula to rewrite the logarithm in terms of natural logarithms. 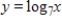
(Multiple Choice)
4.9/5  (30)
(30)
The purchasing power P (in dollars) of an annual amount of A dollars after t years of 4% inflation decays according to 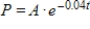 . How long will it be before a pension of $60,000 per year has a purchasing power of $30,000? Round your answer to one decimal place.
. How long will it be before a pension of $60,000 per year has a purchasing power of $30,000? Round your answer to one decimal place.
(Multiple Choice)
4.9/5  (32)
(32)
Evaluate the logarithm by using properties of logarithms and the following facts. Round your answer two decimal places. 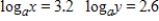
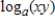
(Multiple Choice)
4.9/5  (28)
(28)
For selected years from 1960 to 2001, the national health care expenditures H, in billions of dollars, can be modeled by 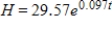 , where t is the number of years past 1960 (Source: U.S. Department of Health and Human Services). If this model remains accurate, in what year will national health care expenditures reach $3 trillion (that is, $3000 billion)? Round your answer to the nearest year.
, where t is the number of years past 1960 (Source: U.S. Department of Health and Human Services). If this model remains accurate, in what year will national health care expenditures reach $3 trillion (that is, $3000 billion)? Round your answer to the nearest year.
(Multiple Choice)
4.8/5  (37)
(37)
Solve the exponential equation. Give the answer correct to 3 decimal places. 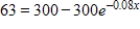
(Multiple Choice)
4.9/5  (39)
(39)
Showing 81 - 100 of 108
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)